时　间：2023 年 10 月 22 日 — 28 日

地　点：天元数学国际交流中心

组织者：田刚、刘小博、郭帅

邀请报告人（按姓氏首字母排序）：

何伟强（中山大学）

柯华忠（中山大学）

李长征（中山大学）

李卫平（香港科技大学）

Alexander Yu Orlov（Insitute of Oceanology RAS）

王军啸（北京大学）

王新（山东大学）

邬龙挺（南方科技大学）

向茂松（华中科技大学）

杨成浪（中国科学院）

杨迪（中国科技大学）

张庆生（北京大学）

张友金（清华大学）

周贝加（北京大学）

周坚（清华大学）

周杨（复旦大学） 

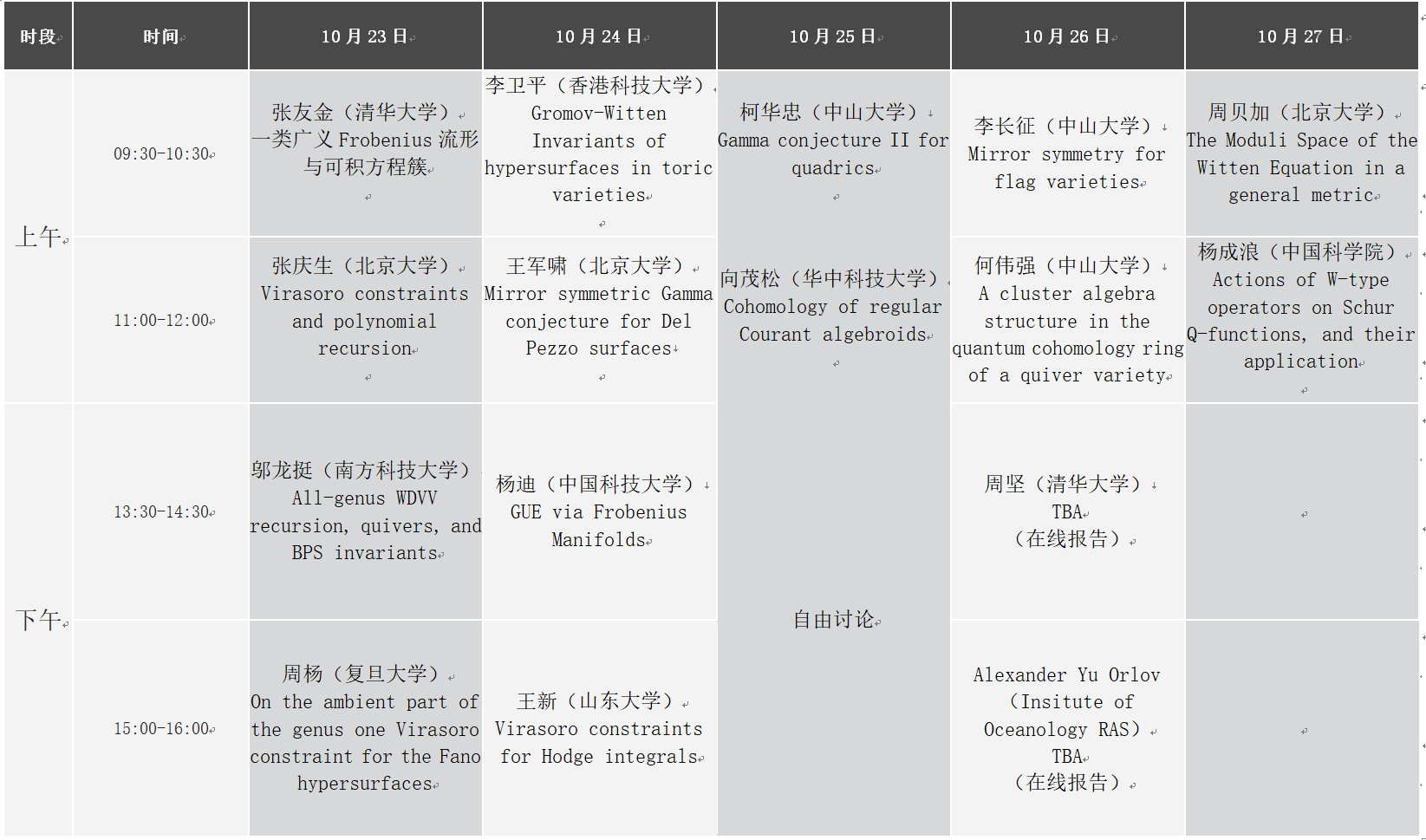
会议日程安排：

报告摘要

A cluster algebra structure in the quantum cohomology ring of a quiver variety

何伟强

中山大学

The Gromov-Witten theory of a quiver variety is expected to be preserved by quiver mutation acording to Seiberg duality, which has been proved to be ture for A-type and star-shaped quivers. On the other hand,cluster algebra can be construced for a given quiver via quiver mutation. Benini-Park-Zhao’s work indicates that there should be a cluster algebra structure in the quantum cohomology ring of a qiuver variety. In this talk, I will discuss the mathematical construction on the cluster algebra structure in quantum cohomology ring of a A_n qiuver variety.

This is a joint work with Yingchun Zhang.

Gamma conjecture II for quadrics

柯华忠

中山大学

Gamma conjecture II for quantum cohomology of a Fano manifold was proposed by Galkin,

Golyshev and Iritani. It expects to describe the asymptotic behavior of flat sections of the Dubrovin connection near the irregular singularity, in terms of a full exceptional collection of and the Gamma-integral structure. We give a criterion for this conjecture, based on Dubrovin’ s result of analytic continuation of semisimple Frobenius manifolds. As an application, we use this criterion to verify this conjecture for smooth quadric hypersurfaces. This talk is based on a joint work with Xiaowen Hu.

Mirror symmetry for flag varieties

李长征

中山大学

In this talk, we will review the current study on mirror symmetry for flag varieties. We will also discuss a folklore mirror symmetry expectation on the eigenvalues of first Chern class, using concrete examples of flag varieties of Lie type A. This is based on a work in progress joint with Konstanze Rietsch, Mingzhi Yang and Chi Zhang.

Gromov-Witten Invariants of hypersurfaces in toric varieties

李卫平

香港科技大学

I will discuss a method in studying higher genus Gromov-Witten invariants of the Calabi-Yau quintic threefolds. I will concentrate on the geometric aspect of the method used, which is called N-mixed spin P-fields. I will also discuss the generalisation of this method to other hyper-surfaces in topic variable by looking at one example. The method and its variations are developed by Huai-Liang Li, Guo Shui, Jun Li, Melissa Liu, Wei-Ping LI and Zhou Yang.

Virasoro operators as ’creation and annihilation’ operators in matrix model

Alexander Yu Orlov 

Insitute of Oceanology RAS

It is a well-known fact that Virasoro generators cancel the partition function of known matrix models. However, using the elements of this algebra, it is possible to create coherent states that describe matrix integrals in the form of series in coupling constants. As examples, we can consider some generalized version of the Kontsevich integral and some two-matrix models (for example, the Panda-Mehta interpolating ensemble).

Mirror symmetric Gamma conjecture for Del Pezzo surfaces

王军啸

北京大学

For a del Pezzo surface of degree ≥ 3, we compute the oscillatory integral for its mirror LandauGinzburg model in the sense of the Gross-Siebert program. We explicitly construct the mirror cycle of a line bundle and show that the leading order of the integral on this cycle involves the twisted Chern character and the Gamma class. This proves a version of the Gamma conjecture for non-toric Fano surfaces with an arbitrary K-group insertion.

Virasoro constraints for Hodge integrals

王新

山东大学

In this talk, we first review Eguchi-Hori-Xiong’s L_n and L˜_n constraints for Gromov-Witten invariants. Then, as a generalization of these two constraints, we propose Virasoro conjecture for Hodge integrals of any smooth projective variety. Finally, we give some recent results on this conjecture.

All-genus WDVV recursion, quivers, and BPS invariants

邬龙挺

南方科技大学

Let D be a smooth rational ample divisor in a smooth projective surface X. In this talk, we will present a simple uniform recursive formula for (primary) Gromov-Witten invariants of OX(−D). The recursive formula can be used to determine such invariants for all genera once some initial data is known. The proof relies on a correspondence between all-genus Gromov– Witten invariants and refined Donaldson–Thomas invariants of acyclic quivers. In particular, the corresponding BPS invariants are expressed in terms of Betti numbers of moduli spaces of quiver representations. This is a joint work with Pierrick Bousseau.

Cohomology of regular Courant algebroids

向茂松

华中科技大学

Differential graded (dg for short) manifolds (a.k.a. Q-manifolds) emerged from a number of areas of mathematics and theoretical physics such as string theory, Hamiltonian mechanics, and derived geometry. Hamiltonian systems in symplectic graded manifolds encodes many interesting geometrical structures. For example, Courant algebroids, introduced by Liu, Weinstein and Xu, can be realized as Hamiltonian systems in symplectic graded manifolds of degree 2. Meanwhile, cohomology of Courant algebroids, defined via dg geometry, plays an important role in the AKSZ’s construction of 3D topological Courant sigma models. For each regular Courant algebroid, we construct a minimal model and a Hodge-to-de Rham type spectral sequence to compute its cohomology. This is a joint work with Cai Xiongwei and Chen Zhuo.

Actions of W-type operators on Schur Q-functions, and their application

杨成浪  

中国科学院

W-type operators appear in realizations of some infinite dimensional Lie algebras, offering symmetries for both the KP and BKP hierarchies. For examples, they give Virasoro operators, cut-and-join operators, and operators in the W-constraints. Schur Q-functions give characters for irreducible projective representations of symmetric groups. In this talk, I will introduce a formula for action of W-type operators on Schur Q-functions. Application to study the expansion of Brezin-Gross-Witten model in terms of Schur Q-functions will also be introduced.

This talk is based on joint work with Professor Xiaobo Liu.

GUE via Frobenius Manifolds

杨迪 

中国科技大学

This seminar, towards understanding interesting relations between matrix models and the Gromov–Witten (GW) theory from a global aspect, consists of three parts. In the first part, we review the GUE (Gaussian Unitary Ensemble) matrix model and give a new proof of a theorem of Dubrovin, establishing a relationship between the GUE partition function and the partition function of GW invariants of the complex projective line, and discuss some of its applications. The proof uses the matrix-resolvent method as well as the Dubrovin–Zhang method. In the second part, based on Dubrovin’s theorem we derive loop equations for the GUE partition function, and show that the GUE partition function is equal to part of the topological partition function of the non-linear Schrödinger (NLS) Frobenius manifold. In the third part, we consider several developments (cluster of Frobenius manifolds, Virasoro constraints, Givental theory) of the above-mentioned results and methods, in particular, we define new analogues of the GUE matrix model.

Virasoro constraints and polynomial recursion

张庆生

北京大学

In this talk, we first derive the Virasoro constraints for ancestor potential of the enumerative geometry. This leads to a polynomial recursion relation, which in semi-simple cases completely determines the generating series of higher genus invariants, extending Gathmann’s result. Then we will propose a generalized Virasoro conjecture for the CohFTs with non-flat units and prove this conjecture in semi-simple cases by using the Givental–Teleman reconstruction theorem.

This talk is based on a joint work with Shuai Guo.

一类广义 Frobenius 流形与可积方程簇

张友金

清华大学

我们考虑一类具有非平坦单位向量场的广义 Frobenius 流形与可积方程簇之间的联系。对任一这样的广义 Frobenius 流形，我们构造了一个流体力学型双哈密顿可积方程簇，并在半单性条件下给出了这一可积方程簇的拓扑形变。作为这一构造的具体例子，我们建立了 Volterra 方程簇以及 Ablowitz-Ladik 方程簇与这类广义 Frobenius 流形之间的联系。

The Moduli Space of the Witten Equation in a general metric

周贝加

北京大学

The Witten equation and its moduli space are the fundamental part of Landau-Ginzburg A model, now its mathematical theory is called FJRW theory. From the beginning, people do not know which metric is best for the Witten equation. Previously H.Fan, T.Jarvis and Y.Ruan used two special conformal constant curvature metrics with |dz| = |z|^α,α = 0,1 near marked points and constructed the virtual fundamental cycle in FJRW theory. In this lecture, I will talk the Witten equation in a general metric, which is conformal constant curvature metrics with |dz| = |z|^α,α < or = 1 near marked points. It contains H.Fan, T.Jarvis and Y.Ruan’sresults as two special cases. I will give the analysis property and Fredholm theory of its moduli space, which can help us to construct its virtual fundamental cycle and a parallel theory to FJRW theory.

Toplogical recursions, Virasoro constraints, and Hodge integrals

周坚

清华大学

A result due to Eynard relates the correlation functions associated with Eynard-Orantin topological recursions to intersection numbers on Deligne-Mumford moduli spaces. We present a new proof based on Virasoro constraints for higher Weil-Petersson volumes due to Kefeng Liu and Hao Xu.

On the ambient part of the genus one Virasoro constraints for Fano complete intersections in projective spaces

周杨

复旦大学

In this talk, we prove a wall-crossing formula for quasimap invariants with weighted markings. Combined with the usual wall-crossing formula for epsilon-stable quasimap invariants, we are able to compare (1) the genus one Gromov-Witten invariants of a hypersurface with ambient insertions and (2) the ϵ = 0+ quasimaps invariants with light markings. The later theory is convex, meaning that it is the nonequivalent limit of some twisted theory for P⁴, which is semisimple. Using that, we are able to verify the ambient part of the genus one Virasoro constraint for the cubic threefold. This is a joint work with Shuai Guo and Qingsheng Zhang.