召集人：程崇庆（南京师范大学）、程伟（南京大学）、尚在久（中国科学院数学与系统科学研究院）、王跃飞（中国科学院数学与系统科学研究院）、

             袁小平（复旦大学）

时间：2024.05.12—2024.05.18

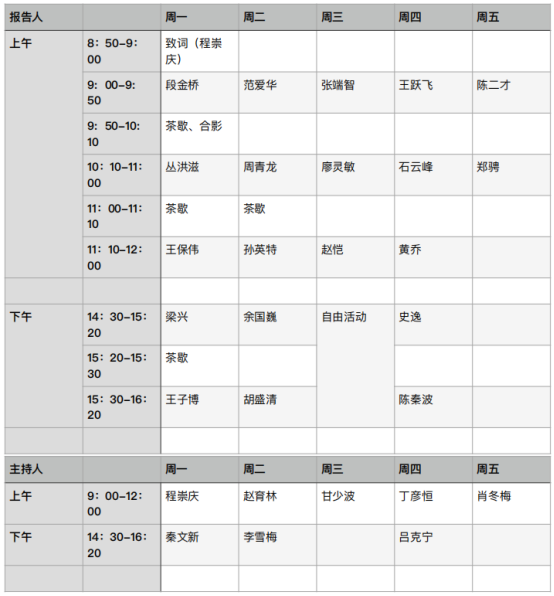
会议日程

报告人简介及报告摘要

段金桥

（大湾区大学）

What Do We Know about Stochastic Hamiltonian Dynamics ?

Abstract: Dynamical systems are often under the influence of random fluctuations. Stochastic Hamiltonian dynamical systems have attracted a lot of attention recently. The interactions between Hamiltonian structures and uncertainty are leading to fascinating dynamical phenomena. The speaker will overview recent advances in stochastic Hamiltonian dynamics, including impact of noise, symplectic vs contact structures, Hamilton’s principle, and effective reduction.

丛洪滋

（大连理工大学）

The existence of full dimensional tori for some Hamiltonian PDEs

Abstract: In this talk, we will discuss the existence of full dimensional tori for some Hamiltonian PDEs

王保伟

（华中科技大学）

Hausdorff dimension for dynamical Diophantine approximation

Abstract: Dynamical Diophantine approximation concerns the Diophantine properties of the distribution of obits in a dynamical system. As far as the Hausdorff dimension is concerned, in many concrete systems, the dimensional formula always shares a common feature, i.e. the solution of the zero of some pressure function. So whether is this a general principle? In this talk, I will speak of the progress on this topic.

梁兴

（中国科学技术大学）

抛物方程传播问题中的动力系统方法

Abstract: TBA

王子博

（华中科技大学）

Small mass limit for Hamiltonian and interacting particle systems under non-Gaussian Lévy noise

Abstract: In this talk, we discuss some limit problems of Hamiltonian and interacting particle systems with non-Gaussian noise, which is helpful for the study of complex high dimensional systems. First, we derive the small mass limit equation for a class of dissipative Hamiltonian systems with Lévy noise. By the symmetric structure of the Hamiltonian system, a noise-induced drift term with Poisson integral form is deduced. When the kinetic energy in the Hamiltonian adopts the classical quadratic form, the Hamiltonian system converges to the limit equation in probability under the Skorokhod topology is provided. Second, we derive the small mass limit equation in the mean field sense for a class of interacting microscopic particle systems with Lévy noise. When the Lévy noise is α-stable, we obtain the limit equation with a convergence rate depending on the non-Gaussianity parameter α.

范爱华

（武汉大学）

Topological polynomial Wiener-Wintner theorem

Abstract: Using the quasi discrete spectrum of Parry-Hahn, we describe topological dynamical systems whose observations are all orthogonal to polynomial weights.

周青龙

（浙江大学）

The positive fundamental group of Sp(2n) and closed geodesics of Hofer's metric

Abstract：In this talk, we examine the homotopy classes of positive loops in Sp(2n). We demonstrate that two positive loops are homotopic if and only if they are homotopic through positive loops. As consequences, we can extend several results of McDuff and Chance to higher dimensional symplectic manifolds without dimension restrictions.

孙英特

（扬州大学）

Stark localization of quantum Hamiltonian operator

Abstract：In this talk, I will introduce Wannier-Stark localization of one body quantum system and many-body Stark Localization of many body quantum system.

余国巍

（南开大学）

Hyperbolic motions in celestial mechanics

Abstract：In the mathematical study of celestial mechanics, some of the most important results are about final motions of the celestial bodies as time goes to infinity. The motion is called hyperbolic if the body goes to infinity with some definite asymptotic direction and no-zero asymptotic velocity, as in the Kepler problem. In this talk, we will report some recent progress for hyperbolic motions in the n-body problem and the restricted n+1 body problem.

胡盛清

（香港中文大学(深圳)）

The long time stability of KAM tori for the derivative nonlinear Schrödinger equation

Abstract：The KAM method is a useful way to prove the existence and stability of quasi-periodic solutions for some PDEs. In 2011, Liu and Yuan obtained the KAM tori for some derivative nonlinear  Schrödinger equation. In this talk, we will discuss the long time stability of these KAM tori.

张端智

（南开大学）

Minimal symmetric period problems in Hamiltonian systems

Abstract: In this talk, we will consider the minimal symmetric period problems in Hamiltonian systems. We give some estimates for the minimal symmetric period of P-symmetric period solutions in semipositive case. For certain symplectic and orthogonal matrix P, in the convex and super quadratic case, we obtain the existence of P-symmetric periodic solution with any given minimal symmetric period.

廖灵敏

（武汉大学）

UNIFORM APPROXIMATION PROBLEMS OF EXPANDING MARKOV MAPS

Abstract. Let T : [0, 1] → [0, 1] be an expanding Markov map with a finite partition. A

H¨older continuous potential ϕ induces an invariant Gibbs measure µ_ϕ. For κ > 0, we investigate µ_ϕ-almost surely the size of the uniform approximation set

U ^κ (x) := {y ∈ [0, 1] : ∀N ≫ 1, ∃n ≤ N, such that |T ⁿx − y| < N ^−κ }.

The critical value of κ such that the Hausdorff dimension of U ^κ (x) equals to 1 for µ_ϕ-a.e. x is proven to be 1/α_max, where α_max = − ∫ ϕ dµ_max/ ∫ log |T′| dµ_max and µ_max is the Gibbs measure associated with the potential − log |T′|. Moreover, when κ > 1/α_max, we show that for µ_ϕ-a.e. x, the Hausdorff dimension of U ^κ (x) as a function of 1/κ agrees with the multifractal spectrum of µ_ϕ. This is a joint work with Yubin He.

赵恺

（同济大学）

Hamilton-Jacobi方程解的Lyapunov稳定

Abstract: 结合接触哈密顿系统的弱KAM方法和哈密顿-雅可比方程的粘性解理论，我们近期研究了接触型哈密顿-雅可比方程粘性解的Lyapunov稳定性和不稳定性。进一步，我们研究了周期解的存在性与多重性。

王跃飞

（中国科学院数学与系统科学研究院/深圳大学）

On the dynamics of p-adic holomorphic maps

Abstract: We will talk about our recent results on the characterization of the global dynamics of p-adic sub-hyperbolic rational maps, and a construction of p-adic rational maps with empty Fatou set. This is joint work with Aihua Fan, Shilei Fan, Lingmin Liao and Hongming Nie.

石云峰

（四川大学）

Anderson localization for multi-dimensional quasi-periodic Schrodinger operators

Abstract: In this talk, we will introduce recent progress on Anderson localization theory  of quasi-periodic Schrodinger operators on Z^d

黄乔

（新加坡南洋理工大学）

Information projection and Onsager--Machlup functional revisited, in connection with Schr\"odinger bridges

Abstract: In this talk, we revisit the constrained information projection with respect to the classical Wiener measure. This information projection corresponds to finding the most probable path of an associated Gibbs measure defined via its Onsager--Machlup functional. We realize the Gibbs measure by a stochastic gradient system, in the two cases when the energy, as a Brownian functional, is either a time integral or a stochastic integral. Both lead to a second-order Hamilton--Jacobi--Bellman equation, which implies that the realization processes are Schr\"odinger bridges. With the help of stochastic geometric mechanics, we build the connections between the Onsager--Machlup minimization problem and the stochastic variational problem with the same Lagrangian through large deviations.

史逸

（四川大学）

The C^r-closing lemmas for partially hyperbolic diffeomorphisms with 1D-center

Abstract: In this talk, we will introduce the C^r-closing lemma and chain closing lemma for partially hyperbolic diffeomorphisms with 1-dimensional center bundle. We will also discuss their applications to understanding the dynamics of such systems in C^r-topology.

陈秦波

（南京大学）

A new perturbation problem for Hamilton-Jacobi equations and its applications

Abstract: In this talk we discuss a new perturbation problem for convex Hamilton-Jacobi equations and study the behavior of the viscosity solutions. In addition, we apply our results to introduce a linear operator, which provides new insight into constructing and characterizing the solutions.

陈二才

（南京师范大学）

Group extensions for random shifts of finite type

Abstract: In this talk, I will present a study on the group extensions for topologically mixing random shifts of finite type and consider the natural comparison of relative Gurevič entropies between random group G and Gab=G/[G,G] extensions. We show that the relative Gurevič entropy of random group G extensions is equal to the relative Gurevič entropy of random group Gab extensions if and only if G is amenable. This is a joint work with K. Yang, Z. Lin and X. Zhou.

郑骋

（上海交通大学）

Jarnik-Besicovitch type theorems for semisimple algebraic groups

Abstract: The Jarnik-Besicovitch theorem in the metric theory of Diophantine approximation states that the set of γ-approximable numbers has Hausdorff dimension 2/(1+γ). In this talk, we discuss a recent result about Jarnik-Besicovitch type theorems for semisimple algebraic groups from the representation-theoretic point of view.