召集人：周向宇（中国科学院数学与系统科学研究院）、Karine Chemla（法国国家科学研究中心）、曲安京（西北大学）

时    间：2024.06.23—2024.06.29

PROGRAM

This conference aims to make senior experts and young scholars gain a global understanding of the history of modern mathematics. All aspects of the history of modern mathematics are welcomed, such as the formation process of mathematics in the 19th century, mathematical proofs in various cultures and times, the relationship between the history and philosophy of mathematics, the history of modern mathematics in the Digital Age, etc. By bringing historians of mathematics together, we hope to explore some frontier problems of the history of modern mathematics in various cultures. The Conveners and Scientific Committee of this conference are as follows:

Sunday, June 23

09:00-18:00    Arrival and Registration 

17:30-19:00    Dinner

Monday, June 24

 Session Chair：Chang Wang

08:30-09:00    Opening Ceremony

1. Opening remarks by Conveners

2. Conference Group Photo

Session Chair：Xi Liu

09:00-09:50  From computation to a practice of proof: Poncelet's ideal elements in geometry

Speaker：Karine Chemla    Université Paris Cité, France

09:50-10:40  Mathematical Structures and Category Theory

Speaker： Sung-Sa Hong    Sogang University, Korea

10:40-11:00    Coffee & Tea  Break

Session Chair：Baoqiang Yang

11:00-11:50  Three Generations of Legacy：Function Theory of Several Complex Variables in China

Speaker： Wenlin Li, Lei Wei    Chinese Academy of Sciences, China

11:50-13:00    Lunch

13:00-14:30    Break

 Session Chair：Wanjuan Du

   14:30-15:20  Definition, vagueness and conceptual development in mathematical practice

Speaker： James Tappenden    University of Michigan, USA

15:20-16:10  Why Historical Research Needs Mathematicians Now More Than Ever

Speaker： Viktor Blasjö    Utrecht University(Holland), Sweden

16:10-16:30    Coffee & Tea  Break、

Session Chair：Lizhen Ji

16:30-17:20    Discussion

17:30-19:00     Dinner

Tuesday , June 25

Session Chair：Pingping Zhang

 08:30-09:20  Poincaré's idea of thinking machines

Speaker：Colin Mclarty    Case Western Reserve University, USA

09:20-10:10  An Inconvenient Proof: Zermelo's well-ordering theorem and its aftermath

Speaker： José Ferreirós    Universidad de Sevilla, Spain

10:10-10:30    Coffee & Tea  Break

Session Chair： Yilin Zhang

10:30-11:20  The construction of Chinese mathematical symbol system： Analysis of "Dai Wei Ji Shi Ji" (Elements of Analytical Geometry and of Differential and Integral Calculus)(1859)

Speaker： Hong Zhang    Sichuan Normal University, China

11:30-13:00    Lunch

13:00-14:30    Break

Session Chair：Jinze Du

14:30-15:20  On E. Study's practice and conception of geometrical objectivity

Speaker： Nicolas Michel    University of Wuppertal (Germany), France

15:20-16:10  Types of quartic equations solved generally in Ars Magna

Speaker：Jiwei Zhao    Northwest University, China

16:10-16:30    Coffee & Tea  Break

Session Chair：Manuel Jesús García Pérez

16:30-17:20     Discussion

17:30-19:00     Dinner

Wednesday, June 26

Session Chair：Xianci Zeng

08:30-09:20  Galois' theory of ambiguity and its impacts

Speaker： Lizhen Ji    University of Michigan, USA

09:20-10:10  Hong Gil-ju and his works on spherical trigonometry

Speaker：Young-Wook Kim    Korea University, Korea

10:10-10:30    Coffee & Tea  Break

Session Chair：Juan Li

10:30-11:20 Why isn't Galois' name on the Eiffel Tower?

Speaker：Anjing Qu    Northwest University, China

11:30-13:00    Lunch

13:00-14:30    Break

14:30-17:30    Discussion

17:30-19:00    Dinner

Thursday, June 27

Session Chair：Xianjun Liu

08:30-09:20  Various quests for totality in the history of mathematics

Speaker： Norbert Schappacher    Université de Strasbourg(France), Germany

09:20-10:10  An in-depth reading of Riemann's Parisian work

Speaker： Yuhui Liu    Hebei GEO University, China

10:10-10:30    Coffee & Tea  Break

Session Chair：Qiang Yang

10:30-11:20  Henri-Léon Lebesgue and the intuitionism of Brouwer: what is the connection between them?

Speaker： Thomas Berthod    Université Paris Cité, France

11:30-13:00    Lunch

13:00-14:30    Break

Session Chair：Zhongmiao Yu

14:30-15:20  Russell against Russell: architectonic issues in The Principles of Mathematics

Speaker： Sébastién Gandon    Université Clermont Auvergne, France

15:20-16:10  Yang K. C.'s doctor dissertation and its academic influence in China

Speaker：Kesheng Chen  Northwest University, China

16:10-16:30    Coffee & Tea  Break

Session Chair：Jiwei Zhao

16:30-17:20    Discussion

17:30-19:00     Dinner

Fridayg, June 28

Session Chair：Wei Chen

08:30-09:20  The origins of the notions of reduced forms and equivalence of forms in the works of Lagrange

Speaker： Cecilia Neve    Universidad de Sevilla, Spain

09:20-10:10  Analysis of hot spots and changing trends in early modern mathemati-cs research in China —— Based on professional mathematics journals from 1949-1966

Speaker： Yu Zhang    Northwest University, China  

10:10-10:30    Coffee & Tea  Break

Session Chair：Hongxing Zhang

10:30-11:20  Comparing Max Noether's and Georges-Henri Halphen's approaches to the reduction of singularities

Speaker： Paul-Emmanuel Timotei    Université Paris Cité, France

11:30-13:00    Lunch

13:00-14:30    Break

 14:30-17:30    Discussion

17:30-19:00    Dinner

Saturday, June 29

Departure

Report Summary

(In alphabetical order of last name)

Henri-Léon Lebesgue and the intuitionism of Brouwer:

what is the connection between them?

Thomas Berthod

Université Paris Cité, France

Abstract: In the philosophy of mathematics there is a particular position, known as intuitionism, which rejects the principle of excluded middle in order to deduce new results. At first sight, the harshness of this approach, introduced by Brouwer at the beginning of the 20th century, may seem surprising. How did Brouwer justify such a position? History seems to have provided him with the perfect means to do so. Brouwer and his proponents turned to the history of mathematics to try to legitimise their position. They identified Emile Borel, Henri Lebesgue and René Baire - a group of French mathematicians from the late nineteenth and early twentieth centuries - as the forerunners of their thought. Brouwer even described them as "pre-intuitionists".

In this way, a relationship is established between Brouwer's ideas on the one hand and those of these French mathematicians on the other. Those who use the term "pre-intuitionism" suggest that the work of these mathematicians should be interpreted from a retrospective point of view, that is, from Brouwer's later thinking. But is there really a connection between these two works? These French analysts presented their work and their philosophical views long before Brouwer. In seeing these mathematicians as forerunners of Brouwer's ideas, are we not falling into the trap of anachronism? Which mathematicians can really be called "pre-intuitionists"? Our talk will raise these questions.

In our presentation, we will focus mainly on the case of Lebesgue. Indeed, in recent works using the term "pre-intuitionism", Lebesgue is explicitly mentioned as a key figure in this movement. However, in the early uses of the term, especially in Brouwer's own work, Lebesgue is not referred to. So why did Lebesgue come to be included in this movement? Is it possible to see Lebesgue's work as a part of this "pre-intuitionism" movement? We will try to answer these questions in our talk.

Why Historical Research Needs Mathematicians Now More Than Ever

Viktor Blasjö

Utrecht University(Holland), Sweden

Abstract: Using the history of the calculus as an example, I identify some trends in recent scholarship and argue that the time is ripe for a "new internalism" in the historiography of mathematics. The field has made steady progress in the past century: mathematicians have provided clear expositions of the technical content of past mathematics, and historians have produced meticulous editions of textual sources. These contributions have been invaluable, but we are reaching a point where the marginal utility of further works of these types is diminishing. It is time to shape a paradigm of historical scholarship that goes beyond the factual-descriptive phase of the past century. Comparative interpretative work is now feasible thanks to the gains of the past century. Cognitive questions about mathematical practice provide a fascinating and underexplored avenue of research that we now have the tools to tackle. Mathematically trained researchers are needed for this enterprise.

From computation to a practice of proof:

Poncelet's ideal elements in geometry

Karine Chemla

Université Paris Cité, France

Abstract: In the late 1810s, Jean-Victor Poncelet began to conceive a research program aimed at making geometrical approaches to geometry as powerful as analytical ones. In this context, Poncelet introduced "ideal" elements, which were given pride of place in his Traité des Propriétés Projectives des Figures (1822). In a first part of this presentation, I will discuss the nature of these "ideal" elements. I will then examine the use of elements of this kind in the practice of proof to which the Traité des Propriétés Projectives des Figures attests. In a third part, I will turn to the notebooks that Poncelet wrote in Saratov, as a prisoner of war, between March 1813 and June 1814, to shed light on the part played by Poncelet's analytical approaches at the time in the genesis of the concept of ideal elements and in that of a new practice of proof in geometry. This talk is based on joint work with Bruno Belhoste.

Yang K. C.'s doctor dissertation and its academic influence in China

Kesheng Chen

Northwest University, China

Abstract: Analytic number theory is to study number theory problems by means of analytic method. It is very important for the development of other branches of number theory, mathematics and even computer science and so on. Analytic number theory was not from China and it was transplanted into China in 1928 by Yang K. C.. So that Yang was reckoned as the first man who transplanted analytic number theory into China. He studied in the University of Chicago of America. His doctor advisor was Dickson L. E.. Yang began to study analytic number theory in 1926. After two years, Yang achieved doctor's degree and so that he was pioneer of analytic number theory in China. Afterwards his pupils acquired the world first achievements in analytic number theory in China. These achievements had some relations with Yang. For examples, Additive Theory of Prime Numbers. It was said that China started to study abroad in mathematics in early part of 20 century and it immensely influenced the development of modern Chinese mathematics. Analytic number theory was one of modern Chinese mathematics. Yang transplanted and led the development of analytic number theory in China. After several generations' hard work, China squeezed into academic frontier in analytic number theory and especially some domain of analytic number theory was broken away from Chinese achievements.

Historical study of analytic number theory in China was payed close attention for researchers in China and abroad. Their studies were to concentrate the achievements of analytic number theory in China and so that by the way mention Yang and his teaching in Tsing Hua University. But previous researches had not been to study Yang's doctor dissertation and not probed academic inheritance of his doctor dissertation in China. This paper will analyze Yang's doctor dissertation--Various Generalizations of Waring's Problem, and then study academic inheritance in China.

For the analyse of Yang's doctor dissertation, two points will be studied: firstly, explaining Yang's doctor dissertation, it had four parts. Part I Representation of all positive integers by 9 pyramidal numbers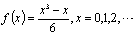 . Part II integers represented by the form 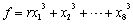where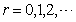 or 8 and each 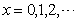. Part III Conditions that a form of degree 7 and weight 143 shall represent all positive integers. Part IV Determination of  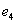 for certain quadratic functions in additive number theory. This also corrected previous errors about Yang's doctor dissertation. Secondly, analyzing Yang's doctor dissertation, mainly is to probing the source about the Four Parts. Extracting and purifying these mathematical thought.

For the academic inheritance of Yang's doctor dissertation, four points will be studied: firstly, studying early Hua Loo-Keng's papers. That is to analyzing the academical relations with Yang and Hua. These papers were Waring's problem for cubes, On Waring's theorems with cubic polynomial summands, and An easier Waring-Kamke problem. Secondly, studying early Ke Chao's papers. That is to analyzing his one paper and his doctor dissertation. His paper was On a Waring's problem with squares of linear forms, and his doctor dissertation is On the representation of a quadratic form as a sum of squares of linear form.Manchester. Thirdly, studying Min Szu-hao's paper--An analogue of Tarry's problem. Fourthly, development of analytic number theory after the People's Republic of China. Especially Chinese mathematicians studied Waring's problems by the way of relay race and succeeded to optimize for Waring's problems. These Chinese mathematicians were Wang Yuan, Pang Cheng-Dong, Chen Jing-Run.

An Inconvenient Proof: Zermelo's well-ordering theorem and its aftermath

José Ferreirós

Universidad de Sevilla, Spain

Abstract: This talk connects with the topics of my chapter in the Richness book, from a more focused point of view - a single proof that caused great stir and was at the origins of the "foundational crisis". After the debate on Cantor's ideas motivated by König in the 1904 ICM at Heidelberg, still in that year, Zermelo published a short paper proving that every set can be well-ordered. Then in 1905 several reactions emerged, including many authors who regarded the proof (and the axiom of choice on which it was based) as inadmissible, for various reasons. The issue of well-ordering and the axiom of choice remained for decades a key source of discomfort for mathematicians, and in particular a source of "second thoughts" about set theory. As a result, figures such as Borel campaigned for more restricted ways of arguing in mathematics, and others like Weyl and Brouwer proposed alternatives to classical set theory. Hence the need to talk about "set theories" in the plural.

Russell against Russell: architectonic issues in The Principles of Mathematics

Sébastién Gandon

Université Clermont Auvergne, France

Abstract: In The Principles of Mathematics (1903), Russell intends to deduce mathematics from logic. This task requires developing logical resources so as to be able to define the main mathematical concepts and prove the main mathematical theorems. But it also requires agreement on the content of mathematics and its organization into disciplines and sub-disciplines. It is this second concern, which I call "architectonic" and which is often neglected in the literature, that I will address in my talk. I will show that it raises delicate questions for both the historian of mathematics and the historian of philosophy.

Mathematical Structures and Category Theory

Sung-Sa Hong

Sogang University, Korea

Abstract: Since Peano (1858-1932) introduced the axioms for the natural numbers, the structural approaches were used in every field of mathematics. One can find the trend in the Bourbaki series and others. It is also well known that underlying structures are revealed by maps preserving the structures, which include the identity maps and are closed under compositions. In the 1970's, category theory was formalized. Using functors between categories, mathematical structures are well established.

Galois' theory of ambiguity and its impacts

Lizhen Ji

University of Michigan, USA

Abstract: Galois is very famous, or best known, for his Galois theory for algebraic equations. On the other hand, he made multiple deep contributions beyond the traditional boundary of algebraic equations.For example, near the end of his testamentary letter, he briefly described his theory of ambiguity. Several distinguished mathematicians such as Lie, Picard, Klein, Dieudonne, Grothendieck have tried to offer their interpretations of this theory. We will discuss these interpretations, point out some potential problems, and describe their impacts. Then we offer a new interpretation and also explain Galois' motivation for this theory of ambiguity. 

Hong Gil-ju and his works on spherical trigonometry

Young-Wook Kim

Korea University, Korea

Abstract: During the 18th century Joseon struggled in accepting the new theory of calendar from Ching. They had to develop totally new mathematics through fragmental documents imported from China. At the beginning of the 19th century Hong Gil-ju was one of the first to successfully decipher the trigonometry on spheres. We explain the history in this development. 

Three Generations of Legacy：

Function Theory of Several Complex Variables in China

Wenlin Li, Lei Wei

Chinese Academy of Sciences, China

Abstract: Function theory of several complex variables is a research field that started earlier in modern China and continues to produce results of international level. This paper describes the founding contribution of Hua Loo-Keng and the research tradition of function theory of several complex variables in China, which has been formed by the work of three generations of Chinese scholars since the nineteen forties, analyzes the academic characteristics of this tradition and its enlightenment on the development and talent training of modern mathematics in China.

An in-depth reading of Riemann's Parisian work

Yuhui Liu

Hebei GEO University, China

Abstract: Riemann's paper on heat conduction in 1861, written in response to a question for a prize from the Paris Academy of Sciences, aroused great interest among mathematicians and historians. The rich ideas contained in this paper, even after more than a century of excavation, has not been exhausted, and has provided new insights and challenges. But this paper is written in an extremely compressed form and is very incomprehensible. For this reason it is necessary to derive every formula in this Parisian work and to trace every mathematical structure back to its origins in order to gain a deeper understanding of Riemann's geometrical ideas.

Poincaré's idea of thinking machines

Colin Mclarty

Case Western Reserve University, USA

Abstract: David Hilbert's Foundations of Geometry in 1899 made Henri Poincaré imagine thinking machines before Hilbert did. Poincaré found the idea ''deadly for teaching, and desiccating for researchers'' but indispensable for telling when intuitions have been fully expressed. Poincaré certainly knew such machines were infeasible when he wrote that. But he inherited boundless faith in science and technology from his family, and their milieu. He knew first hand of the 19th century advances in mechanical calculators and in the punch-card controlled automated looms (which had already inspired Babbage in conceiving of digital programmable computers). This talk explores Poincaré's ideas on thinking machines with emphasis on feasibility.

On E. Study's practice and conception of geometrical objectivity

Nicolas Michel

University of Wuppertal(Germany), France

Abstract: Recent scholarship has fruitfully (re)framed mathematical modernity, at the turn of the 20th century, in terms of a rift in mathematicians' relation to their objects, their language, and to the meaning of their theories (see e.g. Mehrtens 1990, Gray 2008, Corry 2023). Rather than a purely technical crisis in the foundations of mathematics, this scholarship argues, what came under strain at that time was the very definition of mathematics as a scholarly discipline and a way of knowing. New conceptions of what this knowledge is about and of how we gain access to it were emerging and clashing. Some would have mathematics turned into a formal language game, made exclusively of signs and symbols bearing little to no connection to natural or mental objects. Others instead stressed the role of intuition and individual creativity in the formation of this knowledge, and placed embodied cognition and understanding at the forefront of mathematics in lieu of the written text.

The German mathematician Eduard Study(1862-1930) occupies an uneasy position with regard to such narratives of modernity. Alongside David Hilbert, he was a student of Felix Klein: he thus closely worked with two tutelar figures of modern mathematics and their unresolved tensions. A recognized expert in many cutting-edge mathematical theories, from non-Euclidean geometries to Einsteinian relativity and including enumerative methods in algebraic geometry, Study also leveraged his expertise to construct philosophical views of his own in reaction to the aforementioned tensions.

His views, however, reject both horns of the dilemma that many modern mathematicians were then grappling with. Study starkly rejected any appeal to intuition, and condemned vagueness in modern geometrical methods. Only the cold precision of algebraic language, he contended, could propel geometry to the levels of rigor and modernity achieved by analysis or arithmetic. Yet, Study was also a staunch critic of axiomatics, and more broadly of any attempt at making mathematics into a formal game devoid of objectivity, into a discourse that bears on no actual object of knowledge. To restore the complexity and unity of Study's counter-modern views, and to better place them against the backdrop of contemporary debates on mathematical language, cognition, and objectivity, this paper uses a two-pronged approach. First, I explore what I call "object-building practices" in a selection of Study's mathematical publications, namely his Habilitationsschrift on the enumerative theory of conics and his influential reworking of Lie-Klein's line-geometry. In so doing, I analyze what symbolic and geometrical devices Study mobilized to construct, define, and wield the objects described by his mathematical theories. I then compare these practices to Study's Prolegomena zu einer Philosophie der Mathematik, an unfinished typescript on mathematical objectivity preserved in his Nachlass at the University of Bonn. Doing so, I show, sheds new light on Study's critical engagement with a rich philosophical tradition, and on the importance of his own mathematical experience in this process. Furthermore, it enriches our understanding of mathematical modernity as a complex cultural, intellectual, and scientific phenomenon.

The origins of the notions of reduced forms and

equivalence of forms in the works of Lagrange

Cecilia Neve

Universidad de Sevilla, Spain

Abstract: As some of the basic elements underlying the influential theory of quadratic forms, the notions of reduced forms and equivalence of forms are of paramount importance in the development of Mathematics in the 19th century. Although named and exploited by Gauss, we can trace these notions back to Lagrange's "Recherches D'Arithmétique", considered the first systematic study of quadratic forms. However, in order to fully understand this work, along with the origins of these notions, it is necessary to study it as the culmination of a set of works, written by Lagrange in the years 1768-1772.

In this talk we explore these works, tracing the development of ideas that gave rise to these notions, along with the unitary substitutions —linear integer invertible transformations— by which equivalence of forms is defined. We argue that all three notions emerge as an intertwined product of the interaction and joint development of methods, problems, and theory throughout this set of works, preceding as tools and methods the questions posed in the "Recherches D'Arithmétique" that they help to solve.

Various quests for totality in the history of mathematics

Norbert Schappacher

Université de Strasbourg(France), Germany

Abstract: Inspired at first by Alain Herreman's notion of "inaugurational statements" in the history of mathematics, this talk will then substantially modify this approach with a view to attacking a crucial feature of the development of mathematics in the 19th and 20 centuries, which may not have received so far all the attention it deserves: the idea of moduli and moduli spaces. 

Definition, vagueness and conceptual development in mathematical practice

James Tappenden

University of Michigan, USA

Abstract: This paper studies mathematical concepts whose definitions are in some way or other incomplete, requiring additional development before they are entirely grasped. I briefly revisit two previous studies of this phenomenon - Lakatos' study of theorems on regular polyhedra and Peacocke's discussion of what he called the "partial grasp" of the derivative possessed by Newton and Leibniz, and then consider a few additional examples, particularly the concept of the genus of a surface, in which definitions that are provably equivalent in a certain context nonetheless differ in their potential for development and generalization. I consider some ramifications of such examples for the philosophy of language.

Comparing Max Noether's and Georges-Henri Halphen's

approaches to the reduction of singularities

Paul-Emmanuel Timotei

Université Paris Cité, France

Abstract: Georges-Henri Halphen (1844-1889) composed an appendix titled "Etude sur les points singuliers des courbes algébriques planes [Research on the singular points of plane algebraic curves]" for the French translation of George Salmon's A Treatise on the Higher Plane Curves (the translation was carried out by O. Chemin and published in 1884). The third part of this appendix deals with questions regarding the reduction of singularities. Halphen presents a method that was new at the time, and that seems to be forgotten today. This method allows him to obtain the same result for the reduction of singularities of plane curves as the one Max Noether had published a few years earlier. This result, Halphen claims, can be generalized easily and allows him to obtain the following theorem:

For any algebraic curve, one can find a point-by-point correspondence that associates it with another curve on which the points corresponding to all the singular points of the first curve are simple points, and which itself has no other singular points than ordinary double points.

Halphen attributes this statement to Noether and adds:

[My] analysis of [the reduction of singularities given in] nos. 58 and 59 gives Mr Nöther's theorem a more geometric form.

What does Halphen mean with words a more geometric form? My talk will offer an interpretation. Moreover, I will address the following question:

Why does Halphen judge his approach more geometric than Noether's?

To explore this issue, I will present Noether's and Halphen's method of the reduction of singularities, their knowledge about the reduction of singularities. I will suggest that the training Halphen received at the École Polytechnique is a key background to understand his practice of mathematics in the context of the reduction of singularities.

The construction of Chinese mathematical symbol system: Analysis of

"Dai Wei Ji Shi Ji"

(Elements of Analytical Geometry and of Differentialand Integral Calculus)(1859)

Hong Zhang

Sichuan Normal University, China

Abstract: "Dai Wei Ji Shi Ji" (Elements of Analytical Geometry and of Differential and Integral Calculus, 1859) was the first Western calculus book translated into China. The publication of this book not only marks the establishment of calculus discipline in China, but also means the formal establishment of mathematical symbol system in China. Although the mathematical symbol system of "DaiWeiJiShiJi" was widely spread in the late Qing Dynasty, the ways, rules and meaning on construction of mathematical symbol system has not been discussed in depth and systematically.

The construction of mathematical symbol system will be influenced by culture. "DaiWeiJiShiJi" attempted to reconstruct a mathematical symbol system that integrated western mathematics with traditional Chinese mathematics, and made a local transformation of the western symbol system. Therefore, from the cultural perspective, this paper analyzes the way and reason of constructing the mathematical symbol system of "DaiWeiJiShiJi". Secondly, combined with the mathematics practice, the rule and significance of the mathematical symbol system are explored. "DaiWeiJiShiJi" includes algebraic symbols and calculus symbols, which can be used as a typical sample in the process of the westernization of Chinese mathematical symbols. The analysis of its symbol system can provide a glimpse of the cultural conflict and cultural identity in the process of the spread of Western mathematics in China.

Analysis of hot spots and changing trends in early modern mathematics research in China —— Based on professional mathematics journals from 1949-1966

Yu Zhang

Abstract: From 1949 to 1966, more than 10 professional mathematics journals were published as important carriers for the dissemination and circulation of mathematical knowledge in early modern China, and the mathematical articles published by them were the epitome of the development of mathematics in early modern China. Based on the national newspaper index and CNKI databases, this paper collects data, extracts information, converts text, and establishes a text database of professional mathematics journals. On this basis, computer means were used to screen high-frequency word articles, draw a domain relationship diagram of authors, and conduct visual analysis. Then, combined with the in-depth analysis of the authors' community and social background, it is found that due to the influence of national policies and mathematician groups, the research enthusiasm in the field of differential equation theory has gradually increased, and there has always been a high research enthusiasm in calculus. The fields of function theory, topology, functional analysis, and pure mathematics of modern algebra had a certain degree of research enthusiasm in the early years of the founding of the People's Republic of China, but the research enthusiasm was low from 1956 to 1961, and increased from 1962 to 1966.

Types of quartic equations solved generally in Ars Magna

Jiwei Zhao

Abstract: Cardano says in Chapter 39 of Ars Magna that Ferrari and he have found the solutions of all the types of quartic equations without cubic term and those types without linear term. All the 20 types of such quartic equations have been listed out by him.

However, in discussing Ferrari's method, many scholars seem not to take much account for Cardano's own narrative, and they are inclined to think that Ferrari and Cardano had solved all 42 types of quartic equations, i.e., the general quartic equation.

Why so many scholars understand Ferrari and Cardano in such a way? What are the evidences of their argument? Did Cardano give such an implication that they had solved all types of quartic equations if he did not speak definitely?

To answer these questions, we must examine carefully the relevant sections of Ars Magna as well as those of the mentioned literatures. In this talk, we will first discuss the scholar’s explanations of Ferrari and Cardano, then we will turn to the details of what the above two mathematician had done on quartic equations.

After analysis, we get the following conclusions:

Ferrari and Caldano did not give the general method for quadratic equations containing both cubic and linear terms in Ars Magna. They neither completed the fourth power and cubic terms into the square, as in Case 1) of modern method, nor did they use the linear substitution to eliminate the cubic term as in Case 2) of modern method.

Rather, they only solved the 20 types of quartic equations that do not contain both cubic term and linear term simultaneously. Exactly the same as what Cardano had listed out! No evidence shows that they had known the general solutions of the 22 types of quartic equations containing both cubic and linear terms simultaneously. So, when we explain the methods of Ferrari and Caldano for quartic equations, we should not say that they had solved the general quartic equations, nor should we explain them by Case 1) or Case 2) of modern method.

List of Participants

(In alphabetical order of last name)