召集人：李奇睿（浙江大学）、麻希南（中国科学技术大学）、邱国寰（中国科学院数学与系统科学研究院）

时间：2024.12.08—2024.12.14

会议日程

题目和摘要：

l 陈传强(宁波大学)

题目： Strict power convexity of solutions to elliptic Partial Differential Equations

摘要:  The convexity of solutions to elliptic partial differential equations is an important issue. In this talk, we establish some strict power convexity results for fully nonlinear PDEs by the Constant Rank Theorem method, which is a joint work with Haohao Jia，Jiawei Xiong and Yan Ma.

l 高正焕(西安交通大学)

题目: Uniqueness of radial solution to (p, k)-Hessian equation

摘要: In this talk, we concern about a fully nonlinear elliptic (p, k)-Hessian equation. We give a proof of the uniqueness of negative solution to a Dirichlet problem of (p, k)-Hessian eqaution in a finite ball of Rⁿ for 1 < k < n/p. Our proof is based on a Pohozaev identity and the monotome separation techniquess.

l 胡鹰翔 (北京航天航空大学)

题目: Prescribed Lp curvature problem

摘要: In this talk, I will talk about the existence of a strictly convex even solution to the Lp prescribed curvature problem. The key idea is to combine a new gradient estimate with Chou-Wang’s geometric lemma to obtain the C ⁰ and C ² estimate simultaneously. This is a joint work with M.Ivaki(TU Wien).

l 蒋飞达(东南大学)

题目:  Necessary and sufficient conditions on solvability for real (n−1) Monge-Ampère equation in bounded and unbounded domains

摘要: In this talk, we consider the solvability of the (n−1)-Monge-Ampere equation. By imposing proper assumptions on the weight b(x), bounded solutions and large solutions are obtained in the whole Euclidean space Rⁿ. Moreover, the infinite Dirichlet boundary value problem is studied in a bounded strictly convex domain. This talk is based on joint works with Jingwen Ji, Mengni Li and Haiyun Deng.

l 涂绪山 (香港科技大学)

题目: Regularity and classification of the free boundary for a Monge- Ampere obstacle problem

摘要: We study the following Monge-Amp\`ere obstacle problem det D²υ=gυ^qχ_{υ>0}，υ≥0 is convex q∈[0,n）is constant,

which arises from the Lp Minkowski problem.   We prove that the strictly convex part of ∂{υ=0} is C ^1,α if g is bounded away from 0 and ∞, and is C ^2,α and uniformly convex if in addition log g ∈ C ^α. As a result,  when g ≡ 1, we obtain the classification of the global solutions for q = 0, and also for q ∈ (0, n) under the additional assumption that the coincidence set {v = 0} is unbounded. This is a joint work with Tianling Jin and Jingang Xiong.

l 王博 (北京理工大学)

题目: A Serrin-type over-determined problem for Hessian equations in the exterior domain

摘要: I will report a recent work joint with Zhizhang Wang. We consider the Hessian equation in some exterior domain with prescribed asymptotic behavior at infinity and Dirichlet-Neumann conditions on its interior boundary. We obtain that there exit a unique bounded domain and a unique strictly convex  solution to satisfy the over-determined problem.

l 翁良俊 (比萨大学)

题目: Hypersurface curvature flows and isoperimetric-type problems

摘要: We will discuss the hypersurface flows approach to isoperimetric-type problems involving general geometric quantities. The isoperimetric problem for two geometric functionals can be formulated as an optimization problem in the calculus of variations: minimizing one quantity subject to the constraint that the other is fixed. This approach seeks a "good path" that descends to the "optimal solution." For the classical isoperimetric inequality, this naturally leads to a mean curvature type flow. More generally, the approach gives rise to new types of curvature flows. We examine the long-time existence and convergence of these flows for closed hypersurface, as well as compact hypersurface with capillary boundary setting.

l 吴骁天 （浙江大学）

题目： A class of optimal transportation problems in Sⁿ

摘要: In this talk, we will discuss a class of optimal transportation problems in the unit n-sphere, which is characterized by cost functions with singularity and domains with boundary. Aleksandrov problem for open hypersurfaces and refractor design problem are included as two typical examples. We find the necessary and sufficient condition for existence of Aleksandrov weak solutions using properties of the Kantorovich duality functional. We also derive globally smooth solutions by establishing a priori estimates for a parabolic flow towards optimal transportation with nice initial data and constructing approximating initial data. This talk is based on a joint work with Professor Qi-rui Li.

l 吴汪哲 (中国科学院数学与系统科学研究院)

题目: σ_k Yamabe measure

摘要: Trudinger-Wang introduced the notion of k-Hessian measure associated with  k-convex functions, not necessarily continuous, and proved the weak continuity of the associated k-Hessian measure with respect to  local L¹ convergence in 1999. In this paper we find a special divergence structure for the σ_k-Yamabe operator, and prove the weak continuity of the σ_k-Yamabe measure with respect to  local L¹ convergence.

l 夏超 (厦门大学)

题目: Reilly-type integral formula and applications

摘要: We discuss generalizations of Reilly-type integral formula and their applications in various geometric problems.

l 杨志鹏 （云南师范大学）

题目：Heat kernel on 2-step stratified Lie groups

摘要：I will present some basic analysis results on 2-step stratified Lie groups G. In particular, based on explicit knowledge of the irreducible unitary representation of G, I will perform a Fourier analysis of the sub-Laplacian and give a closed formula for the heat kernel of the sub-Laplacian on G.

l 叶剑 (中国科学院数学与系统科学研究院)

题目: Local rigidity of minimal hypersurfaces with constant scalar curvature in S⁴

摘要: In this talk, we are concerned with minimal hypersurfaces with constant scalar curvature in S⁴ In 1987, Almeida-Brito showed that each closed hypersurface  with constant mean curvature and nonnegative constant scalar curvature in S⁴ was isoparametric.  The nonegativity of scalar curvature was established by S. P. Chang. In 1993, Bryant conjectured that each minimally immersed hypersurface of constant scalar curvature in S⁴ is isoparametric. We introduce the recent development on Bryant conjecture.

l 袁伟 (中山大学)

题目: On the Gauss-Bonnet-Chern formula on Poicare-Einstein manifolds

摘要: Gauss-Bonnet-Chern formula is a remarkably fundamental result which builds a connection between differential geometry and topology. It has been successfully generated on Poicare-Einstein manifolds through renormalized curvature integral by Albin. With the aid of ambient space construction, we give a general formulism for renormalized curvature integral. In particular, we give a reformulation of Guass-Bonnet-Chern formula on Poicare-Einstein manifolds, which provides some interesting applications. This work is a joint work with Jeffrey S. Case, Ayush Khaitan, Yueh-Ju Lin and Aaron J. Tyrrell.

l 张会春 (中山大学)

题目 ： Boundary regularity of harmonic maps from RCD(K,N) spaces to CAT(0) spaces

摘要: In this talk, we shall introduce some improvements of the regularity theoryfor harmonic maps from RCD(K,N)-spaces to CAT(0) spaces, including the interior regularity and the boundary regularity. This is a joint work with Professor Xi-PingZhu. 

l 张伟 (兰州大学)

题目： Constant rank theorems for convex solutions of special Lagrange equations

摘要: In this talk, we will discuss the fully nonlinear elliptic equation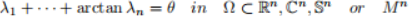 

Where 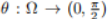   is a given function. Under certain structural condition, we establish several types of constant rank theorems that extend the earlier results of Caffarelli, Guan, and Ma [Comm. Pure Appl. Math., 2007], Li Qun [Indiana Univ. Math. J., 2009], and others.

l 张翼 (中国科学院数学与系统科学研究院)

题目： Alexandrov’s theorem and Serrin’s problem: Weak solutions and quantitative stability

摘要: The Alexandrov theorem states that, any compact hypersurface embedded in Rⁿ with constant mean curvature is necessarily a sphere. Meanwhile, Serrin's problem concerns a class of overdetermined issues within the framework of partial differential equations. In this talk, we discuss about the relations between these two theorems, highlighting recent developments in their weak formulations and exploring the quantitative stability results.

l 周斌 (北京大学)

题目 : Applications of the partial Legendre transform in Monge-Amp\`ere type equations

摘要: In this talk, I will report the recent progress on the applications of partial Legendre transform in the Monge-Amp\`ere equation, linearized Monge-Amp\`ere equations as well as Monge-Amp`ere type fourth order equations.

l 周星晨 (清华大学)

题目 : New approaches in a priori estimates for prescribing scalar curvature equations

摘要: The interior a priori estimates are important issues in the study of prescribing scalar curvature equations and quadratic Hessian equations.  Various techniques are developed in this area, among them the most well-known one is the pointwise argument that apply maximal principle to an elaborate auxiliary function. There are also integral ways using  rotation and/or mean value inequalities. All these approaches require the C ² norm of the right hand side. So we ask a question which is natural to all fully nonlinear second order partial differential equations: can one obtain C ²α  estimates that depends only on C ^α norm of the right hand side? In this talk we present an new integral approache for prescribing scalar curvature equations and quadratic Hessian equations, that will take one step toward this question. The talk is based on a joint work with Chen Ruosi and Jian Huaiyu, and also a resent paper of myself.