召集人：周向宇（中国科学院数学与系统科学研究院，研究员）、Konstantinos Nikolantonakis（希腊，UNIVERSITY OF WESTERN MACEDONIA，教授）、萨日娜（上海交通大学，教授）

时间：2025.06.22—2025.06.28

Schedule

Sunday，June 22

Monday Morning，June 23

Monday Afternoon，June 23

Tuesday Morning，June 24

Tuesday Afternoon，June 24

Wednesday Morning，June 25

Wednesday Afternoon，June 25

Thursday Morning，June 26

Thursday Afternoon，June 26

Report Summary

Shang Gao’s Mathematical Ideas

ZHOU Xiangyu

Abstract：Ancient Chinese mathematics is “simple in words but deep in meaning”. In this talk, we will provide an overview of Shang Gao's mathematical ideas and achievements:

1) explain Shang Gao's theorem, and restore Shang Gao's proof of the GouGu theorem (勾股定理) by recalling Shang Gao's key ideas and methods in the proof: “ZheJu (折矩)”“JiJu (积矩)”“JiFangZhi (既方之)”“HuanErGongPan (环而共盘)”;

2) explain more Shang Gao's one idea of “ZheJu (折矩)” and its applications (including 容横容直原理、重差术;

3) explain Shang Gao's proof by XianTu (弦图) and its consequences (product-difference/product-sum problem积差/积和问题、relation between geometric mean and arithmetic mean) ;

4) explain the ideas of Shang Gao and ancient Chinese on motion，infinity and limit （方圆-圆方术：origin of GeYuanShu割圆术）；

5) explain the “shape-body invariants (形体不变量)” idea of Shang Gao and Zhao Shuang.

Liu Hui and Heron of Alexandria calculate areas and volumes: two examples from Chinese and Hellenistic mathematical traditions

Konstantinos Nikolantonakis

University of Western Macedonia

knikolantonakis@uowm.gr

In this paper we are going to discuss some methods proposed by Liu Hui and Heron of Alexandria for calculating areas and volumes. Liu Hui’s methods are in an algorithmic way. Heron, applies a geometrical analysis part (in the Euclidean way) and an arithmetical – algorithmic synthesis part. By studying two specific examples (trapeziums and truncated pyramid) we are in front of similarities and differences of the methods used in the context of these two mathematical traditions: the Chinese and the Hellenistic.

再论吴文俊院士的数学史遗产

李文林

（中国科学院数学与系统科学研究院）

本文在作者《论吴文俊院士的数学史遗产》的基础上进一步论述吴文俊院士数学史观的历史意义。

1、关于数学史上的两种主流或倾向；

       i.倾向性与排他性；

      ii.主流性与唯一性

2、关于“出入相补原理”；

3、案例分析——两种传统下对无理数的认知。

       结语

Revisiting Academician Wu Wen-Tsun’s Legacy

in the History of Mathematics

LI  Wenlin

The Academy of Mathematics and of Systems Science, CAS

This article further elaborates on the historical significance of Academician Wu Wen-Tsun’s perspectives on the history of mathematics, building upon the author’s previous work, “On the Academician Wu Wen-Tsun’s Legacy in the History of Mathematics”.  

1. On the Two Mainlines or Tendencies in the History of Mathematics  

    i. Tendency and Exclusivity

    ii. Tendency and Uniqueness

2. On “the Out-In Complementary  

     Principle”

3. A Case Study—The Understanding of Irrational Numbers under the Two Traditions  

  Conclusion

中西开方术及其思想的比较研究

郭世荣  

(内蒙古师范大学科学技术史研究院)

摘要：开平方、开立方是中国传统数学中的重要内容，《九章算术》给出开平方、开立方、开带纵平方、开带纵立方的筹算程序和算法，到宋元时代出现了开高次方的立成释锁开方法和增乘开方法，秦九韶《数书九章》（1247年）在解高次方程时根据系数和开方过程中系数的变化情况给出各种开高次方法。成书于1202年（1228年修订）的意大利数学家斐波那契的《计算之书》（Liber Abaci）是中世纪欧洲数学的标志性著作。该书第14章专门讲述开平方和开立方算法。至于开高次方法，在西方则要等到公元1819年英国中学教师霍纳的相关论文，这被视为西方数学史上的重要事件。本篇报告比较东西两种文化传统的开方术，分析其中体现的数学思想，指出二者的共同点与不同点，从而阐明二者间所代表的不同的逻辑推理起点和思想方法。

关键词：开方术，《九章算术》，斐波纳契《计算之书》，比较研究

A Comparative Study of Chinese and Western Extraction of

Roots and Their Thoughts

Guo Shirong

(Institute for the History of Science and Technology, Inner Mongolia Normal University)

Abstract: The calculation procedures for finding square roots and cubic roots are important contents in traditional Chinese mathematics. The programs and algorithms were recorded in Jiuzhang suanshu (Nine Chapters on Mathematical Procedures). During the Song and Yuan dynasties (AD. 960-1368), the methods for extraction of a higher degree roots were developed, such as the methods of licheng shisuo fa (root extraction of using table) and the zengcheng kaifang fa (extraction methods of using addition and multiplication). In his Shushu jiuzhang (Nine Chapters of Mathematical work, 1247), Qin Jiushao developed various extraction procedures of roots, based on different coefficients of extraction expressions and the changes in coefficients during extraction  process. In the western mathematics, the Liber Abaci, written by Italian mathematician Leonardo Pisano Fibonacci in 1202 (revised in 1228), is a landmark work of the medieval European mathematics. Chapter 14 of the book specifically discusses the square root and cubic root. As for the method for extraction of high-degree roots, William Horner, a British high school teacher, developed so-called Horner’s rule in a paper published in 1819 , which is considered an important result in the history of Western mathematics. The present paper will compare the root extraction techniques of the two cultural traditions in the East and the West, analyze the mathematical ideas reflected in them, point out their similarities and differences, and thus elucidate the different logical reasoning starting points and thinking methods represented by the two.

Keywords: extraction of a root, Jiuzhang suanshu, Fibonacci’s Liber Abaci, comparative study

刘徽对《九章算术》中立体的辨名

邹大海 夏庆卓

（1.中国科学院自然科学史研究所，北京100190；2.中国科学院大学,北京100049）

摘要：刘徽对《九章算术》中的立体及其名称进行了较多的考察，是他对全书概念、术语进行“审辨名分”工作的组成部分，也是他努力为《九章算术》的数学知识构建理论基础的一种体现。本文分为不做解释、只解释实物含义、只解释几何含义、既解释实物含义又解释几何含义等四种类型分析了刘徽对《九章算术》中立体及其名称和用语的处理方式，指出刘徽对立体进行的辨名工作是一个重大的进步，但还未能形成作为基础的一套解释术语和一个解释框架，是不完善的。尽管如此，刘徽的辨名工作仍足以为他论证数学方法的正确性提供基础。

关键词： 刘徽，《九章算术》，立体，辨名，中国古代数学理论

 A Study on Liu Hui’s Work of Distinguishing the Names of the Geometric Solids in the Nine Chapters on Mathematical Procedures

ZOU Dahai ¹   XIA Qingzhuo ^1,2

(1．Institute for the History of Natural Sciences, Chinese Academy of Sciences, Beijing 100190; 2. University of Chinese Academy of Sciences, Beijing 100049)

Abstract: Liu Hui examined the geometric solids and their names of the Nine Chapters on Mathematical Procedures, which is an integral part of his work of “examining the meaning of words and distinguishing their scope” on the concept and terminology of the book, and is also an embodiment of his efforts to construct a theoretical basis for the mathematical knowledge of the book. This paper adopts four ways to analyze Liu Hui’s treatment of the solids and their names or descriptions in the Nine Chapters on Mathematical Procedures: no explanation, only explaining the meaning of material object, only explaining the meaning of geometry, explaining both the meaning of material object and the meaning of geometry. It is pointed out that Liu Hui’s work on distinguishing the names and their meanings of the geometric solids is a major advance, but his work is not perfect for he did not form a set of explanatory terms and a framework for interpretation. Nevertheless, Liu Hui’s work is enough to provide the basis for him to demonstrate the correctness of the mathematical methods.

Keywords: Liu Hui; Nine Chapters on Mathematical Procedures; geometric solid; distinguishing names; ancient Chinese mathematical theory.

Realizing Liu Hui's reasoning--Place Values and Geometric Reasoning in Root extraction procedure in the Song commentary to the Nine Chapters of Mathematical Art
Jeff Chen

（明尼苏达州圣克劳德州立大学）

In studying the Song (960-1279) commentary to root extraction procedures in the Nine Chapters of Mathematical Art (九章算術，jiuzhang suanshu), we discovered a new way of keeping track of place values on the counting surface. Such a finding ascertains and connect the stages in its geometric reasoning with the steps in the procedure. Moreover, the geometric reasoning also explains why the procedure is also applicable in finding the root of certain quadratic equations. A related issue is the practice of using concrete examples to describe general procedures in Chinese mathematical treatises.

Mathematical Expressions of Sangaku and Books by Schools  in the Edo Period 

Noriko TANAKA
（Naragakuen University, Nara, Japan）

During the Edo period (1603-1867), the shrines and temples of Japan began to display amongst their artifacts votive mathematical tablets. These tablets were known as Sangaku [算額]. These mathematical tablets and books were illustrated with beautiful geometry diagrams in addition to problems, answers and solution outlines. They are written in the kanbun [漢文] language, a form of classical Chinese with Japanese readings. When we read kanbun, we add symbols such as 一, 二 or レ and read in a different order to classical Chinese.

There were several schools of mathematics in Japan during the Edo period. The most famous and popular school was the Seki school [関流] of the renowned mathematician Seki Takakazu [関孝和] (?-1708). In addition to the Seki school, there were various other schools such as Takuma school [宅間流], Shisei-Sanka school [至誠賛化流], Saijyo school [最上流] etc.

The mathematical books and tablets were written in different expressions in different schools. The Seki school's way of expressing mathematics is inspired by the motif of Sangi [算木] (arithmetic sticks), which was introduced from China to Japan. The Sangi were placed vertically for the first, hundred, and ten thousand places and horizontally for the tenth, thousand, and hundred thousand places. The red blocks represent positive numbers, and the black blocks represent negative numbers. When writing in books, negative numbers were represented by diagonal lines to express them in black ink only. In addition, zero is expressed by ○. For example, || 一○ represents 210.

Takuma school was a school founded by Takuma Yoshikiyo [宅間能清] in Osaka. Takuma school does not use numerical expressions of arithmetic sticks. Negative numbers are written as fu (フ) in Japanese katakana [カタカナ], and numbers are one (一), two (二), three (三) in Japanese kanji [漢字]. Shisei-Sanka school was a school founded by Hurukawa Ujikiyo [古川氏清](1758-1820). The meaning of the phrase “Shisei-Sanka [至誠賛化]” is to agree that heaven, earth, and nature create and nurture all things if one is sincere in one's heart. The expression of the formula is almost the same as the expression of Seki school's formula.

Furthermore a license was required to teach Japanese mathematics in the Edo period. A person who is granted a license can teach mathematics. Depending on the type of license, the content of mathematics that could be taught differed. Some licenses allow teaching only basic mathematics, while others enable teaching complicated mathematics. Note that the license is kept wrapped up.

The notation of the Wasan [和算] (Japanese Mathematics in the Edo period) is inspired by Chinese writing and Sangi. The Seki school was the largest, but it is interesting to note that the schools did not unify their methods of expression until Western mathematics reached and changed to it.

招差术“立法之意”：清中后期数学家傅九渊“招差术解”

高红成

（天津师范大学数学科学学院；天津师范大学科学技术史与文化遗产研究院）

傅九渊，江西上高人，是清代中后期数学家。根据新的史料考证，他生于1791年，卒于1845年。1821年中举，1823年进士，1837—1838年任湖北远安县知县。1845年任山东长山县知县，未到任所便去世了。他对算学颇有研究，著有《有不为斋算学》（4卷）。其中卷一“招差术解”和卷二“（招差）算例”，这两卷专论招差术的立术之原，完成于1822-1823年间。从目前所见算书中，这两卷是第一部专论招差术的专著。书中傅氏相当于明确指出招差术是用高阶等差数列(包括等差数列)各阶差分首项表示通项公式（多项式）以及求和公式的方法，并明确指出差分首项各系数与贾宪三角形斜行数字之间的对应关系。从现存史料来看，傅九渊是我国第一位把招差术数学意义表述清楚的数学家。

The Legislative Intent of the Finite Difference Method: A Study on Fu Jiuyuan's Explanation of the Finite Difference Method in the Mid-Late Qing Dynasty

GAO Hongcheng

（School of Mathematics, Tianjin Normal University, Tianjin 300387, China; Institute for Cultural Heritage and History of Science &Technology，Tianjin Normal University， Tianjin 300387, China）

Fu Jiuyuan （傅九渊）, a native of Shanggao, Jiangxi, was a mathematician in the mid-late Qing Dynasty. According to new historical records, he was born in 1791 and died in 1845. He became a juren (successful candidate in the imperial provincial examination，举人) in 1821, obtained the jinshi (metropolitan graduate,，进士) degree in 1823, and served as the magistrate of Yuan'an County, Hubei from 1837 to 1838. In 1845, he was appointed magistrate of Changshan County, Shandong, but died before assuming office.

He conducted profound research in mathematics and authored Arithmetic of Youbuwei Zhai (4 volumes)（《有不为斋算学》，Youbuwei Zhai  (Studio of "Not Doing Certain Things") was the name of Fu Jiuyuan's study room. ）. Among them, Volume 1 Explanation of the Method of Zhaocha method ( Finite Differences，招差术) and Volume 2 Calculation Examples of Finite Differences  specifically discuss the foundational principles of the finite difference method, completed between 1822 and 1823. Based on current mathematical works, these two volumes represent the first monograph dedicated to the finite difference method. In the book, Fu clearly states that the finite difference method uses the first terms of each order of differences in higher-order arithmetic sequences (including arithmetic sequences) to express the general term formula and summation formula, and explicitly identifies the corresponding relationship between the coefficients of the first terms of differences and the diagonal numbers in Jia Xian's triangle (Pascal's triangle). According to existing historical records, Fu Jiuyuan was the first mathematician in China to clearly articulate the mathematical significance of the finite difference method.

A shared interpretation of celestial origin 天元 in the works of Qin Jiushao and Li Ye

Karine Chemla

School of mathematics (The University of Edinburgh)

&

SPHERE (CNRS & Université Paris Cité)

Thirteenth century Chinese mathematical works attest to two interesting innovations. Qin Jiushao’s 秦九韶  Mathematical Work in Nine Chapters (Shushu Jiuzhang 數書九章, 1247) describes an algorithm solving congruence equations in ways related to the so-called “Chinese remainder theorem”. Moreover, Li Ye’ 李冶 Measuring the Circle on the Sea-Mirror (Ceyuan haijing 測圓海鏡, 1248) shows how to use polynomial algebra to establish algebraic equations solving mathematical problems. Both authors make use of the same technical expression: “one establishes one heavenly source/origin … li tian yuan yi … 立天元一….”. Historians of the past have relied on modern interpretations of the texts to draw the conclusion that, in the two contexts, this expression had different technical meanings. I suggest interpreting this expression in light of the ancient Chinese mathematical canon and its commentaries. This approach allows us to perceive a common meaning to the expression in the two mathematical contexts and, more importantly, to bring to light a tradition of formal work on operations to which a series of Chinese mathematical documents attests.

《谢察微算经》新探

冯立昇

（清华大学科学技术史研究所 内蒙古师范大学科学技术史研究院）

《谢察微算经》是被《新唐书·艺文志》著录的一部古代数学著作，其成书年代当在北宋之前。但以往在一些通史性的中国数学史著作却较少介绍或提到这部算书，只是在一些与珠算史相关的著述中有所论及。近二、三十年，该书才受到数学史界的重视，在中国数学史著作有所介绍，但相关研究还不够全面深入。

本文从文献学和数学两方面对该书进行了全面考察，通过梳理宋代文献有关《谢察微算经》的记载和分析现存残本的内容，确定其成书年代为五代末期，并说明它具有重要的数学价值与文献价值。尽管《谢察微算经》大部分内容已经散失，但保存下来的残文仍然包含了重要的珠算史料和数学史料，不仅确切记载了穿档有梁算盘，而且对珠算术语或用字给出了明确的解释，此外书中还包含一些之前数学著作所没有数学内容，是十分珍贵的数学史料。

New Research on Xie Chawei Suan Jing

FENG Lisheng

（Institute for the History of Science and Technology & Ancient Texts, Tsinghua University; Institute for the History of Science and Technology, Inner Mongolia Normal University）

Xie Chawei Suan Jing （谢察微算经）is an ancient mathematical work recorded in the Xin Tang Shu·Yiwen Zhi（《新唐书·艺文志》），and its writing date should be before the Northern Song Dynasty. However, in some general historical works on the history of Chinese mathematics, this book was rarely introduced or mentioned, and was only discussed in some writings related to the history of abacus calculation. In the past 20-30 years, this book has only received attention from the mathematical history community and has been introduced in some works on the history of Chinese mathematics, but the related research is not comprehensive and in-depth enough.

This article comprehensively researches the book from the textual and mathematical perspectives. By reviewing the records of Xie Chawei Suan Jing in Song Dynasty literature and analyzing the content of existing fragments, it is determined that the book was written in the late Five Dynasties period, and explained this book has important mathematical and literary value. Although most of the content of Xie Chawei Suan Jing has been lost, the surviving fragments still contain important historical materials on abacus and mathematics, such as the record of the abacus with a beam, the clear explanations for abacus terminology or wording. In addition, this book also contains some mathematical content that was not included in previous mathematical works, which has very valuable mathematical historical value.

Influence of Chinese mathematical civilization on Japanese mathematics in the Edo period

Soga, Shohei

　（Seki Kowa Institute of Mathematics, Yokkaichi University）

In the early Edo period, Chinese mathematical books such as the Suanxue Qimeng《算學啓蒙》, the Yang Hui Suanfa《揚輝算法》 and the Suanfa Tongzong 《算法統宗》 were introduced to Japan. Although they were created at different times and had different mathematical civilizations, they were introduced at almost the same time. Furthermore, the introduction of the Tongwen Suanzhi《同文算指》, an adaptation of a Western mathematical book, also came at the same time.　However, it was difficult for Japanese mathematicians at the time to understand the Chinese mathematical civilization that these mathematical books were imbued with, and it took a considerable amount of time to digest them.

Among them, the first thing that Japanese mathematics accepted was methodology. It is recorded that Cheng Dawei's Suanfa Tongzong, published in 1592, was referenced in Yoshida Mitsuyoshi's Jinkoki《塵劫記》, published in 1627. Then, in 1675, a version with Japanese annotations revised by Yuasa Tokuyuki was published. The Suanfa Tongzong was especially valued as a book on Zhusuan［珠算」. The use of both Zhusuan and the ancient Chinese Rod calculus［籌算］ was one of the characteristics of Japanese mathematics in the Edo period, and was a methodology that the Japanese adopted.

The next step was the adoption of a view of mathematics. For example, Zhu Shijie's Suanxue Qimeng was published in 1299, was followed by a Japanese translation by Hisada Gentetsu in 1658, an annotated version by Hoshino Sanenobu in 1672, and an explanatory book by Takebe Katahiro in 1696.  In Takebe's book, "Tengenshu［天元術］" was featured, and the Chinese view of mathematics was understood and developed.

In addition, from the perspective of mathematical civilization, it is necessary to analyze the philosophy, which is a world view, and the bearers of the civilization. In ancient China, mathematics was one of the six arts［六芸］ that served as the education of the scholar-officials［士大夫］, and was also a subject for the promotion examination［科挙］. In this case, the bearers of mathematics were high-ranking government officials. The main academic field they needed to study was the philosophy of mathematics, and they had little interest in its practical application. However, after the Song Dynasty, the private economy in China developed, and there was a demand for people who could carry on mathematics that could be put to practical use. These mathematics books from the Song Dynasty and after were introduced to Japan in the early Edo period. With no scholar-officials or imperial examinations, Japan was in a period of private economic development, and people looked to Chinese books for mathematics that could be put to practical use.

In this presentation, I will analyze historical materials on "Influence of Chinese mathematical civilization on Japanese mathematics in the Edo period" from four perspectives: philosophy, views on mathematics, methodology and bearers. I will also consider its influence on Japan and its development.

中国古代数学的回归

朱一文

（中山大学）

以往关于数学本质的研究大多依赖欧洲及现代数学的历史。本文通过考察非西方数学史（尤其是中国数学史）指出，算筹等物质数学工具不仅影响着数学实作方式，更形塑了实作者从数学活动中获得的知识形态。而儒家算法传统则展现出另一条数学发展路径。因此，中国数学史不仅对理解数学本质具有价值，更为拓展现代数学领域提供了思想资源。中国古代数学遂可被视作一种"补充数学"。

The Return of Ancient Chinese Mathematics

Most previous studies on the nature of mathematics have primarily focused on the history of European and modern mathematics. Drawing on studies of the history of non-Western mathematics, particularly Chinese mathematics, this paper argues that material mathematical instruments, such as counting rods, influenced not only the way mathematics was practiced but also the mathematical knowledge practitioners gained from their practice. In contrast, Confucian mathematical methods represent a different approach to the development of mathematics. Therefore, the history of Chinese mathematics is not only valuable for understanding the nature of mathematics but also for expanding the domain of modern mathematics. Ancient Chinese mathematics can thus be described as a form of "complementary mathematics."

从“黄平象限”到“白平象限”

——清代日食推算中时差符号分界的改变

张祺，宋芝业

（内蒙古师范大学科学技术史研究院，内蒙古呼和浩特 010022）

传统历法长期以“正午”为时差符号分界，然而此方法忽略了黄赤道季节位置差异，导致理论误差。明末《崇祯历书》引入“黄平象限”（黄道距地平最远点）概念，批判旧法“正午”分界的局限，并逐渐被梅文鼎等本土历家所接受。《历象考成》则进一步改进，提出以“白平象限”（白道距地平最远点）为时差符号依据。从正午、黄平象限到白平象限的演变，反映了中国学者在视差理论上从经验性向数理化的转型，揭示中西天文学交融对中国传统历算的影响。

Research on the Process of Changing the Demarcation Point of Time Difference Symbols from "HuangpingXiangxian" to

"BaipingXiangxian" in Solar Eclipse Calculations

in the Qing Dynasty

ZHANG Qi， SONG Zhiye

(Institute for the History of Science and Technology, Inner Mongolia Normal University, Hohhot 010022, Inner Mongolia)

Traditional calendars had long used "Zhengwu"  (正午) as the demarcation point for time difference symbols. However, this method ignored the seasonal positional differences between the ecliptic and equator, leading to theoretical errors. In the late Ming Dynasty, the ChongzhenLishu introduced the concept of "HuangpingXiangxian" (黄平象限) , criticizing the limitations of the old method's "Wuzheng" demarcation, which was gradually accepted by native calendar scholars such as Mei Wending. The Lixiang Kaocheng further improved this by proposing "BaipingXiangxian" (白平象限) as the basis for time difference symbols. The evolution from Zhengwu to HuangpingXiangxian and then to BaipingXiangxian reflects the transformation of Chinese scholars' parallax theory from empirical to mathematical, revealing the influence of the integration of Chinese and Western astronomy on traditional Chinese calendar calculations.

从天文学工具到独立学科：

文艺复兴时期三角学的理论建构与范式转型

曹婧博

（中国科学技术大学科技史与科技考古系，安徽 合肥 230026）

摘要：文艺复兴时期三角学的发展遵循两条主要的历史路径，一方面是“三角形问题”研究开始脱离附属于天文学的地位，从形式独立、功能扩展与术语革命三个方面，完成了从天文计算工具向独立数学学科的理论构建。这一过程既包含正弦定理、球面三角法则等核心三角理论的体系化，也体现出三角形问题从“技艺”到“科学”的范式革命。另一方面，三角形问题的实用性也在文艺复兴时期不断凸显，其广阔的应用范围受到当时数学家约翰·迪伊的重点关注和讨论。研究文艺复兴时期三角学的发展，在探讨数学学科发展史、三角学的实用和理论价值以及数学知识的传承与融合方面具有重要意义。

关键词：三角学；文艺复兴；雷格蒙塔努斯；约翰·迪伊；雷蒂库斯

From Astronomical Tool to Independent Discipline: Theoretical Construction and Paradigm Shift of Trigonometry in the Renaissance Period

CAO Jingbo

Abstract: The development of Renaissance trigonometry followed two main historical paths. On the one hand, the study of the triangle's side and angle problems has begun to detach from its subordinate status in astronomy. Through systematic theoretical construction and a triple transformation of disciplinary paradigms—formal independence, functional expansion, and terminological revolution—trigonometry completed its evolution from an astronomical computational tool into an independent mathematical discipline. This process not only involved the systematization of core theories such as the sine theorem and spherical trigonometric principles but also embodied a paradigm revolution in mathematical cognition, transitioning from a "craft" (ars) to a "science" (scientia). On the other hand, the practicality of the study of triangles was also highlighted during the Renaissance, and its wide range of applications were focused on and discussed by John Dee, a mathematician at the time. The study of the development of Renaissance trigonometry is of great significance in exploring the history of the development of mathematical disciplines, the practical and theoretical value of trigonometry, and the inheritance and integration of mathematical knowledge.

Key words: trigonometry; Renaissance; Regiomontanus; John Dee; Rheticus

数学家曾炯之生平和学术活动考辨

唐家欢¹   杨静^1，2

（1、天津师范大学数学科学学院，天津，300387；

2、天津师范大学科技史与文化遗产研究院，天津，300387）

摘  要  曾炯之（1898–1940）是中国最早从事抽象代数研究的数学家，他曾在抽象代数奠基人埃米•诺特的指导下学习数学，于1934年获得德国哥廷根大学的博士学位。然而关于这位重要数学家的一些基本情况却有不同的说法。本文依据新发现的哥廷根大学档案、旧报刊及相关研究文献等资料，考察和分析了曾炯之的生平和学术活动的几个重要方面：出生及逝世时间，早年的学习经历，留学德国哥廷根大学期间的学习情况，归国后在浙江大学的情况等，希望以此厘清现有记载中的模糊之处，并更为准确地阐述其在中国现代数学发展中的贡献。

关键词  曾炯之  生平  哥廷根大学  浙江大学

A Study on the Life and Academic Activities of Mathematician Chiungtze C. Tsen

TANG Jiahuan¹   YANG Jing^1,2

(1.College of Mathematical Science，Tianjin Normal University， Tianjin 300387，China.

2. Institute of Science and Technology History and Cultural Heritage, Tianjin Normal University，Tianjin 300387，China)

Abstract  Chiungtze C. Tsen(1898–1940) was a pioneering Chinese mathematician who conducted research in abstract algebra. He studied under Emmy Noether, one of the founders of modern abstract algebra, and received his doctoral degree from the University of Göttingen in 1934. Nevertheless, some key details of this significant mathematician’s life and career remain inconsistently documented. This study employs newly discovered archival materials from the University of Göttingen, historical journals, and relevant scholarly literature to investigate and analyze several critical aspects of his life and academic career, including the dates of his birth and death, his early educational background, his period of study at the University of Göttingen, and his academic activities following at Zhejiang University in China. This paper aims to clarify ambiguities in existing records and provide a more accurate account of Tsen's role in the development of modern mathematics in China. This paper aims to clarify ambiguities in existing records and provide a more accurate account of Tsen's role in the development of modern mathematics in China.

Keywords   Chiungtze C. Tsen, Life, University of Göttingen, Zhejiang University

文明的对话与张力：基于中西与印西数学交流的跨文化模式反思

王颖

数学知识的跨文化传播不仅是纯粹知识的流动，更体现为不同文明之间深刻的对话与张力，这一过程总是嵌于具体的历史文化语境和权力结构之中。本文以电影对东西方数学交流现象的表现作为切入口，从清代康熙朝与英属印度时期两个典型历史场景出发，比较分析了数学知识与艺术表现形式、数学家形象塑造之间的相互作用。在康熙时期，数学被纳入以天文历法为核心的国家治理体系，数学家多以官员与实用专家的形象呈现，数学成为一种权力工具和文化象征。而在殖民背景下的印度，数学家拉马努金则以个体天才与神秘直觉的独特形象进入西方数学主流，其艺术化的叙述揭示了数学知识与文化身份建构之间复杂而紧张的关系。这种对比分析为数学史研究提供了文明对话视角，强调应超越西方中心的传统叙事，重新评价非西方数学的历史贡献与文化内涵。

Dialogues and Tensions between Civilizations: Two Cross-Cultural Models of Mathematical Exchange in Sino-Western and

Indo-Western Contexts

WANG Ying

The cross-cultural transmission of mathematical knowledge embodies profound dialogues and tensions among civilizations, invariably embedded within specific historical, cultural contexts and power structures. Using cinematic representations of East-West mathematical encounters as an entry point, this paper comparatively examines the interplay between mathematics, artistic expressions, and the constructed images of mathematicians in two historical scenarios: Qing China under Emperor Kangxi and colonial-era India. In Kangxi's era, mathematics was institutionally appropriated within state governance frameworks emphasizing astronomy and calendar reforms; mathematicians were depicted as officials and practical experts, positioning mathematics as both an instrument of authority and cultural symbolism. In colonial India, however, Srinivasa Ramanujan emerged through narratives emphasizing individual genius and mystical intuition, highlighting the complex tensions in mathematical knowledge transmission and cultural identity formation. This comparative analysis advocates a civilizational-dialogue perspective in mathematical historiography, proposing to transcend Eurocentric narratives and reassess the historical contributions and cultural significance of non-Western mathematical traditions.

Euclid and Archimedes: a study on the forms and uses of the “method of exhaustion”

Guilherme Luiz 丁海亮

The so-called “method of exhaustion”, proved on the Elements, Book X, Theorem 1, is widely used on Book XII of the Elements when Euclid shows a lot of equalities between ratios of volumes and areas (and also one equality between volumes, Elements XII, 10). This same “method of exhaustion” was also used by Archimedes across all his major works related to geometry.

On this talk, we will investigate the patterns behind the proofs in Book XII of the Elements that uses the method of exhaustion. Also, we will investigate some theorems across Archimedes work and try to find a common group between all these demonstrations. At the end, we will summarize our findings on both authors and compare their methods of proof with a special attention to the proof's concerning the sphere: Elements, Book XII, Theorem XVIII for Euclid and About Sphere and Cylinder I, 33-34 for Archimedes.

明清之际地球周长每度里数确立方式探讨

刘增强

（内蒙古师范大学科学技术史研究院，呼和浩特，010022）

摘  要：明清之际的古籍中，有“在天一度在地二百里”、“在天一度在地二百五十里”等数据，此前学者对这些数据的源头已梳理。文章尝试探讨罗明坚、利玛窦、汤若望等来华传教士确定地球周长每度数值的过程。通过研究提出罗明坚、利玛窦来华早期确定地球周长每度里数的三种可能方式；考证阐释利玛窦更改地周每度里数的方式、原因，以及对明末“里”长的认识，并对《利玛窦札记》中的相关内容作了注解；文章还解释了汤若望《浑天仪说》中的相关内容，比较了几种地球周长每度里数值。最后梳理考察了明清之际士人对地周每度里数值的认识，同时揭示了士人对“里”长数值的漠视。

关键词：二百五十里；二百里；罗明坚；利玛窦

Establishing the Li-per-Degree Ratio of Earth's Circumference in Late Ming and Early Qing China: Methods and Contexts

 LIU Zengqiang

(Institute for the History of Science and Technology，Inner Mongolia Normal University，Hohhot，010022)

Abstract: Historical records from the Ming-Qing transition period, such as “one celestial degree corresponds to 200 terrestrial li” or “one celestial degree corresponds to 250 terrestrial li,” have been studied by previous scholars regarding their origins. This article explores the processes by which Jesuit missionaries in China, including Michele Ruggieri, Matteo Ricci, and Johann Adam Schall von Bell, determined the value of the Earth’s circumference per degree. It proposes three possible methods used by Ruggieri and Ricci during their early years in China to calculate this value. The study investigates Ricci’s revision of the li-per-degree ratio, analyzes his rationale for the adjustment, and clarifies late Ming understandings of the li unit, with annotations on relevant passages in China in the sixteeth century: the journals of Matteo Ricci. Additionally, it interprets Schall von Bell’s Hun Tian Yi Shuo and compares various historical estimates of the Earth’s circumference per degree. Finally, the article examines how late Ming and early Qing scholars perceived these values and highlights their general disregard for the numerical definition of the li unit.

Key Words: 250 Li; 200 Li; Michele Ruggieri; Matteo Ricci

秦楚九九简牍管窥

夏庆卓/XIA Qingzhuo ^1,2 邹大海/ZOU Dahai ¹ 

（1.中国科学院自然科学史研究所，北京100190；2.中国科学院大学,北京100049）

摘  要：九九是数字计算的基本工具，在中国有着悠久的历史。目前已知秦朝及以前的出土九九简牍有7件，均来自秦、楚两地。这些九九可分为纯口诀式、纯表格式和带有表格特征的口诀式三种类型。纯口诀式九九出现最早，纯表格式九九属于比较少见的类型，带有表格特征的口诀式九九出现相对较晚，大致到了秦代已成为主流。另外，九九的特征与书写材料有关但并不完全对应。

关键词：北大秦简；秦家咀楚简；里耶秦简；九九；清华楚简

A Study of the Jiujiu for Multiplications on Qin and Chu Bamboo or Wooden Slips

XIA Qingzhuo, ZOU Dahai

Institute for the History of Natural Sciences, Chinese Academy of Sciences

Abstract: The jiujiu (九九, a collection of expressions for basic multiplications in China) is a basic tool for numerical calculation. It has a long history in China. So far, there are 7 pairs of jiujiu bamboo or wooden slips unearthed from the Qin Dynasty and before, all from the tombs of Qin Dynasty or Chu State. These jiujiu can be divided into three types: pure mnemonic rhyme, pure table, and mnemonic rhyme with table features. The first type of jiujiu appeared the earliest, the second type is relatively rare, and third appeared relatively late but had become the main type in the Qin Dynasty. In addition, the characteristics of various jiujiu are related to the writing materials, but this relationship is not a complete correspondence.

Key words: Qin bamboo slips preserved at Peking University; Chu bamboo slips excavated from Qinjiazui; Qin bamboo or wooden slips excavated from Liye; jiujiu (a collection of expressions for basic multiplications in China); Chu bamboo slips preserved at Tsinghua University

The Rise of Traditional Japanese Mathematics and

 Chinese Abacus Books

Ogawa, Tsukane

Seki Kowa Institute of Mathematics, Yokkaichi University

Abstract: The first half of the 17th century was the period of the rise of traditional mathematics in early modern Japan. The most significant influence on it was undoubtedly Chinese mathematics. Especially in the early period, the impact of abacus methods during the Ming Dynasty was substantial. In Japan, the "Iwami Ginzan Silver Mine" was discovered in 1527 in Shimane Prefecture, and the technology of refining silver with lead was introduced from Korea in 1533, leading to a rapid increase in silver production. This silver flowed into the Ming Dynasty through Korea and the Ryukyus. Japanese paid for the goods from Fujian Province via Ryukyu. The first Japanese people who understood the abacus calculation method may have been merchants during trade in the last half of the 16th century, but the details are unclear. Japan got the abacus calculation technique and the books on abacus calculation from the Ming dynasty.

We can find the following Ming dynasty books in Japan today.

1. Xinke jiachuan mijue panzhu suanfa shimin liyong (新刻家伝秘訣盤珠算法士民利用), 2Vol. (1573), Cabinet Library

2. Shuxue tonggui (数学通軌) (1578), Nagaraku no Chikuji, Quray Chuanjing, Maeda Sonkeikaku Bunko

3. Xinbian Zhizhi suanfa tongzong (新編直指算法統宗), 17 Vol. (1592), by Cheng Dawei (程大位) , reprinted in Japan (1676)

4. Xinbian zhizhi suanfayao (新編直指算法要), 4 Volumes (1595), Cabinet Library

5. Suanxue xinshuo (算学新説) (1603) by Zhu Zaiyu (朱載堉) 楽全書附巻, Maeda Sonkeikaku Bunko

6. Suanhai shuoqun (算海説群) (1659)

7. Xinjuan tianxia beilan wenlin leiji wanshu cuibao (新鐫天下備覽文林類記萬書萃宝), volume 36, Waseda Univ. Ogura Library

8. Xinjuan jiuzhang guiyijue suanfa (新鐫九章竜易訣算法), Volume 1, Cabinet Library

9. Kaoshi quanshu (考実全書), Volume 18 Suanfamen (算法門), National Diet Library

10. Xuefu quanbian学府全編, Volume 14 Suanfamen (算法門), Astronomical Observatory

11. Zhizhi suanfa zuanyao (直指算法纂要), 4 Volumes, Cabinet Library

12. Suanfa zhinan (算法指南), Li-Jian Library

Among these books, the Suminokura Ryoi (1554-1614), Suminokura Soan (1571-1632), and Yoshida Mitsuyoshi (1598-1673) studied the seventeen volumes of "Xinbian Zhizhi Suanfa Tongzong (新编直指算法统总)," who, in particular, Yoshida Mitsuyoshi, published the results as the book Jinko Ki (1627’s preface). This book improved the computational ability of the entire Japanese population. After that, Seki Takakazu's (1645?-1708) method of the expression of equations and the theory of elimination of unknowns in simultaneous higher-order equations led to the rapid development of mathematics in Japan.

This lecture will give an overview of the abacus methods of the time and the civil engineering, commerce, and finance based on them, as well as an introduction to the book SuanYongJi (算用记) (1610?-1624) and the book GeSuanShu (割算书) (1622), before the Jinko Ki. I will present some research issues. For example, there are various abacus methods, and it is still unclear how the Japanese method relates to the Chinese method. In Japan, there was a business custom in which 96 coins were threaded onto a string and accepted as 100 coins. This business custom required a good command of the Japanese abacus technology when exchanging money. We cannot find the origin of such a custom.

架设历史学家与数学家之间的桥梁

季理真

（University of Michigan, USA）

中国数学有着悠久而丰富的历史，蕴含着许多宝贵的智慧，可以为数学教育和学生培养提供重要的启示，从基础教育到大学及研究生阶段。因此，一个关键问题是：

*如何在历史学家与数学家之间架设桥梁？* 本次会议汇聚了众多研究中国数学史的专家，他们的报告必将为这一问题提供深刻的见解。

在我的报告中，我将通过以下三个主题探讨这一问题：

   - *中国剩余定理与局部-整体原理：* 讨论局部-整体原理在数论中的重要性及广泛性，以及它与中国剩余定理的联系如何提供新的视角。

   - *刘徽计算 π 的方法与离散-连续原理：* 将刘徽的工作置于这一更广泛的框架中，可以看出它预示了拓扑学中的重要概念和方法。

   - *克莱因-庞加莱之争及单值化定理的历史：*

   我将重点探讨克莱因与庞加莱之间著名的竞争，以及他们对单值化定理历史发展的贡献，展示历史学家与数学家的互动如何推动数学史研究的进步。

通过这些讨论，我希望提供新的思考视角，以更好地理解历史遗产如何融入现代数学教育，并为数学的未来发展提供启发。

Building bridges between historians and mathematicians

Chinese mathematics has a long and rich history, containing many valuable insights that can offer important lessons for education and student development, from primary education to university and graduate studies. Therefore, a key question arises: *how can we build a bridge between historians and mathematicians?* This conference brings together numerous experts in the history of Chinese mathematics, whose presentations will undoubtedly provide profound insights into this question.

In my talk, I will explore this issue through three key topics:

   - *The Chinese Remainder Theorem and the Local-Global Principle:* I will discuss the importance and ubiquity of the local-global principle in number theory and how its connection with the Chinese Remainder Theorem offers a fresh perspective.

   - *Liu Hui’s Work on Computing π and the Discrete-Continuous Principle:*Placing Liu Hui’s work within this broader framework highlights how it foreshadowed key concepts and methods in topology.

   - *The Klein-Poincaré Competition and the History of the Uniformization Theorem:* I will focus on the famous competition between Klein and Poincaré and their contributions to the history of the uniformization theorem, illustrating how interactions between historians and mathematicians drive progress in the study of mathematical history.

Through these discussions, I hope to offer new perspectives on how historical heritage can be integrated into modern mathematical education and inspire future mathematical developments.

Seeking the Sources of the "Nine Chapters on the Mathematical Art":Comparative Study on the Ancient Mathematical Books from the Qin to the Western Han Period

Makoto TAMURA

(Osaka Sangyo University)

  The "Nine Chapters on the Mathematical Art" is a milestone in ancient Chinese mathematics, where the date of completion of the original texts has not yet been determined. However, it was in 263 CE that Liu Hui edited and annotated the original text, giving it the form of a proper mathematical textbook.

  Before that, the following 4 ancient mathematical texts existed. In order of discovery, the Suan Shu Shu from the Zhangjiashan (186 BC), the Shu housed at Yuelu Academy (212 BC), the Shu Shu from the Shuihudi (157 BC), and the Suan Shu housed at the Peking University (216 BC). All of these texts were written on bamboo slips. Although photographic images of the Shu Shu from Shuihudi have not yet been published, the other three texts have provided significant insight into the nature of Chinese mathematics during the Qin to the Western Han periods.

Among these three books, we can observe mathematical problems that can be considered as the sources of some problems in the Nine Chapters. In this talk, we will discuss common and non-common mathematical problems and explore the aspects of the development of ancient Chinese mathematics.

东西方对“毕氏三元数组”的认识：一个跨文明的比较研究

纪志刚

上海交通大学科学史与科学文化研究院

摘  要

一般说来，如果三个非负整数a, b,  c, 满足a² +b²= c²，则a, b,  c被称为“毕达哥拉斯三元数组”（Pythagorean triple，简称“毕氏三元数组”），其中牵涉两个重要问题：

1，在何种条件下三元数组（a, b,  c,）满足a² +b²= c²，此即毕达哥拉斯定理，在中国称之为“勾股定理”。

2，如何推求满足a² +b²= c²的三元整数组，即“毕氏三元数组”，在中国亦即“整勾股数”。

本篇报告将讨论古代文明对毕达哥拉斯定理的认识和对毕氏三元数组的推求。

一、欧几里得《原本》中的毕氏定理和毕氏三元数组

欧几里得《原本》卷I命题47是毕达哥拉斯定理，但毕氏三元数组要在卷X命题29中才给予讨论。命题29有两条引理，引理1是：试求二平方数，使其和也是平方数。

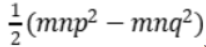希思（T.L. Heath）在引理1下的注记指出，欧几里得给出了构成整数直角三角形的方法。即：设两个相似面数mnp², mnq²，它们同时为奇数或同时为偶数，它们的差除以2，即据卷II命题6，可得：；由此可知：m²n²p²q²，满足条件，即它们的和也是平方数。

此处m, n 被称为欧几里得参数（Euclid’s parameterization）

二、巴比伦泥板的“毕氏三元数组”

普林顿322号（Plimpton 322）曾被认为是一块“商业账单”，但诺伊格鲍尔(O. Neugebauer)将其从六十进制转换为十进制数字后发现泥板中的数字满足毕氏三元数组。1980年，被“数学考古学”所吸引的C·巴克（C. Buck）发表论文Sherlock Holmes in Babylon（AMM.vol.87）。但是，20年后，E·罗布森（E. Robson）的论文Neither Sherlock Holmes nor Babylon: A Reassessment of Plimpton 322（Historia Mathematica, vol.28,2001）中对此做出了严肃的回应。罗布森认为：“如果我们要全面理解古代数学文本和人工制品，就必须从它们的数学历史背景出发来看待它们，而不是把它们当作侦探小说风格的人工的、独立的创作。”罗布森提供了一个基于 “互反数对” (reciprocal pairs) 的更合理的Plimpton 322重构。

三、“整勾股数”在中国：周公的天地之问

与《九章算术》的“二人同所立”

        在《周髀算经》开篇，周公向商高问道“夫天不可得阶而升，地不可得尺寸而度，请问数安从出？”商高借此机会向周公演示了勾股定理的证明：“既方之，外半其一矩，环而共盘，得成三四五。”

《九章算术》的勾股章“二人同所立”题，则给出了推求整勾股数的一般公式。

今有二人同所立。甲行率七，乙行率三。乙东行，甲南行十步而邪东北与乙会。问甲、乙行各几何？

荅曰：乙东行一十步半；甲邪行一十四步半及之。

术曰：令七自乘，三亦自乘，并而半之，以为甲邪行率。邪行率减于七自乘，余为南行率。以三乘七为乙东行率。置南行十步，以甲邪行率乘之，副置十步，以乙东行率乘之，各自为实。实如南行率而一，各得行数。

若令：甲行率为m, 乙行率为n, 在直角三角形中，设若， ，则有：

这就是术文给出的公式。这一结论相当于给出了整勾股弦三者的一般表达式：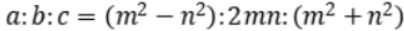

更有意义的是，刘徽在注释中给出了严格的几何证明（李继闵：《刘徽对整勾股数的研究》，《自然辩证法通讯》，1981.5）

四、结语：从勾股之法到勾股算术

本文最后指出：中算家们并没有仅仅满足“勾股定理”或“整勾股数”，他们以勾、股、弦及其差和互求，演变出一套完整的“勾股算术”系统。《数理精蕴》（1722）记载了“求勾股弦无零数法”，开启了中西数学交流新的一页。

因此，以历史之悠久，内容之丰富，知识之系统，应用之广泛，成果之深刻，特色之鲜明，中国古代的“勾股术”是其他任何文明都无可比拟的。从这个意义上来说，斯威兹（F. Swetz）是对的：Pythagora is  Chinese.

Knowing Pythagorean Triples in the East and the West:

A Cross-Civilizational Comparative Study

JI Zhigang

School of History and Culture of Science, Shanghai Jiao Tong University

Generally speaking, if three non-negative integers a, b, and c satisfy a² + b² = c², then a, b, and c are called a “Pythagorean triple”, also known as “integer Gou-gu numbers” in China, and there are two important issues involved:

1. Under what conditions does the triple (a, b, c) satisfy a² + b² = c², which is the Pythagorean theorem, also known as the "Gou-gu theorem" in China.

2. How to find the triples of integers (a, b, c) that satisfy a² + b² = c², this means that the formula of Pythagorean triples, or integer Gou-gu numbers, should be created.

Part I Pythagorean theorem and Pythagorean Triple in Euclid’s Element

In Euclid’s Element Book I, Proposition 47 is the Pythagorean theorem, but the Pythagorean triple appears in Book X Proposition 29, Lemma 1: To find two square numbers such that their sum is also square.

T. L. Health pointed out that Euclid’s method of forming right-angled triangles integral number is as follows: 

Take two similar plane numbers, e.g. mnp², mnq², which are either both even or both odd, so that their differences is divisible by 2. Now by Book II. 6, the product of the two numbers mnp²× mnq², or (mnpq)², is square:

so that the numbers of mnpq,  satisfy the condition that sum of their squares is also a square number.

Here m, n is called the Euclid’s parameterization

Part II Pythagorean triples in Babylonian Tablet

Plimpton 322 was once thought to be a “commercial account”, but after O. Neugebauer converted the numbers on the tablet from base 60 to base 10, he found that the numbers on the tablet satisfied Pythagorean triples. In 1980, C. Buck, attracted by “mathematical archaeology”, published the paper “Sherlock Holmes in Babylon” (AMM, vol. 87). However, 20 years later, E. Robson's paper “Neither Sherlock Holmes nor Babylon: A Reassessment of Plimpton 322” (Historia Mathematica, vol. 28, 2001) made a serious response to this. Robson argued that “Ancient mathematical texts and artefacts, if we are to understand them fully, must be viewed in the light of their mathematico-historical context, and not treated as artificial, self-contained creations in the style of detective stories.”

Part III Integer Gou-gu Numbers in China: From Zhou-bi to Nine Chapters

In the opening of the Zhou-bi Suan Jing, Duke Zhou asked Shang Gao: “The sky cannot be climbed by steps, and the earth cannot be measured by dimensions. Where do numbers come from?” Shang Gao took this opportunity to demonstrate the proof of the Gou-gu theorem to Duke Zhou. Shang Gao replied “Therefore fold a gnomon so that the base is three in breadth, the altitude is four in extension, and the diameter is five aslant. Having squares on its two sides, halve one gnomon(矩). And rotating it around the center to form a square. The result is 3, 4, and 5.”

In the Gou-gu chapter of the Nine Chapters,  the problem ,“two persons standing at the same place” gives a general formula for finding integer Gou-gu numbers.

[9.14] Suppose there are two persons standing at the same place. A walks at the rate of 7, B walks at the rate of 3. B walks to the east, A walks to the south 10 bu and then [turns and walks] diagonally northeast until meeting B.

The question: How far do both A and B walk?

The answer: B walks east 10 1/2 bu. A walks diagonally (邪行) 14 1/2 bu to reach B.

The method: Let 7 (m) be multiplied by itself(m²), and 3(n) also be multiplied by itself(n²), combining [these] and halving [the result], this serves as the rate at which A walks diagonally ( ,邪行率). Subtracting the diagonal walking rate from 7 multiplied by itself (), the surplus serves as the rate [at which A] walks south（ , 南行率）. Multiply 3 by 7 as the rate at which B walks east (n×m, 東行率).

The method indeed gives the general formula for finding integer Gou-gu numbers:

More importantly, Liu Hui provided a strict geometric proof in his commentary.

Part IV Conclusion: From the Gou-gu Theorem to Gou-gu Arithmetic

The article concludes by pointing out that Chinese mathematicians did not merely satisfy themselves with the integer Gou-gu numbers. They developed a complete Gou-gu arithmetic system based on the hypotenuse, the two legs, and their differences and mutual relationships. The book Mathematical Essence（《数理精蕴》，1772）recorded the“method for finding Gou-gu-xian without fractions”（求勾股弦无零数法）, opening a new chapter in the exchange of mathematics between China and the West.

Therefore, in terms of its long history, rich content, systematic knowledge, wide application, profound achievements, and distinct characteristics, the ancient Chinese “Gougu method” is unparalleled by any other civilization. Just in this sense, F. Swetz might be correct: Pythagoras is Chinese.

混合数学视角下的中国古代概率思想探析

王幼军

（上海师范大学哲学系，上海，200234）

摘 要：长期以来，对数学史的研究主要集中在“纯粹数学”（pure mathematics）的发展上，近年来这种情况发生了显著的变化，这些变化的引擎来自于数学史研究的视角、范围和方法等方面所取得的重要进展。其中，最显著的进展之一是被称为“混合数学”（mixed mathematics）的领域正受到越来越广泛的关注，从混合数学的角度考察数学的历史，为以往被数学史研究所忽视的一些内容和重要领域提供了崭新的维度和启示。相应地，古典概率（classical probability）作为一种混合数学，其历史比任何其他数学分支吸引了更多的历史学家的关注；更为有趣的是，混合数学的视角也为重新审视中国古代数学提供了更为丰富的比较背景和新的维度。本文将基于这一视角，重点考察中国古代概率数学即“决疑数学”的思想，并进一步简要讨论这种新的数学史研究视角对中国古代数学本质特征的重新认识及其普遍意义和价值。

关键词：混合数学，中国古代数学，概率，决疑数学

On the probabilistic thinking in ancient China from the mixed mathematics perspective

WANG  Youjun

(Department of philosophy, Shanghai Normal University, Shanghai, 200234)

Abstract:  For a long time, the study for the history of mathematics has mainly focused on the development of "pure mathematics". This situation has changed in recent years, which is brought by some remarkable research advances in the perspective, form, content and method of the study for the history of mathematics. One of the most notable developments is that the field called "mixed mathematics" is receiving more and more extensive attention. Examining the history of mathematics from the perspective of mixed mathematics has provided very new historical dimension and valuable insights into some topics and important areas previously neglected by the study for history of mathematics. Consequently, the history of classical probability theory as a kind of mixed mathematics, has attracted more interest from historians than any other sub-discipline of mathematics. More than that, the perspective of mixed mathematics could also offers a richer comparative context for reassessing ancient Chinese mathematics. From such a perspective, this paper would focus on examining the idea of probability mathematics in ancient China, which was called Jueyi mathematics(决疑数学)，and further giving a brief discussion on the new understanding for essential characteristic features of ancient Chinese mathematics and its universal significance and value brought by this new historical research approach of history of mathematics.

Key words:  Mixed Mathematics; ancient Chinese mathematics; Probability; Jueyi Mathematics

中日传统测量方法的比较研究

——从《日高图》到《日月高测》的历程

萨日娜，梁铭心

上海交通大学科学史与科学文化研究院

摘要：中国古代对太阳高度的测量研发了一种特殊的测量方法，其中既有勾股相关内容，还有一种独特的立杆测影方法。后来又演变成“重差术”这种测远和测高的测量方法。这种测量方法在世界文明史上也是独具特色的。中国传统测量方法随着中日的交流传播到日本，对他们传统数学中的测量方法产生了重要影响。本文首先对《周髀算经》中的“日高图”的测量方法进行解读，再探讨其发展和刘徽《海岛算经》中的测量方法；其次，通过对一些史料的分析考察中国传统测量方法在古代日本的传播，以及在江户时期日本的传承和发展。将研究的重点放在江户时期的著名学者中根元圭《日月高测》中的测量方法和技术上，以此探讨中日传统测量方法的关联性和不同的发展路径。

关键词：日高图；重差术；勾股测量；《日月高测》 

A Comparative Study of Traditional Measurement Methods in China and Japan——The Journey from the Rigao Tu(日高图) and Jitsugetsu Kousoku(日月高测)

Sarina，Liang Mingxin

School of History and Culture of Science, Shanghai Jiao Tong University

Abstract: In ancient China, a special measurement method was developed for the measurement of the sun's altitude, which contains Gougu(勾股) and a unique method of measuring shadows from a pole. Later, it evolved into the method of double differences, for measuring distance and height, which is unique in the history of world civilisation. Traditional Chinese measurement methods spread to Japan with the exchanges between China and Japan, and had an important influence on the measurement methods in their traditional mathematics. In this paper, we first interpret the measurement method of “Rigao Tu(日高图)” in the Zhoubi Suanjing(周髀算经), and then discuss its development and the measurement method in Liu Hui's Haidao Suanjing(海岛算经). Secondly, we examine the dissemination of the Chinese traditional measurement method in ancient Japan, and the inheritance and development of the measurement method in Japan in the Edo period through the analysis of the historical materials. The study focuses on the measurement methods and techniques in the Jitsugetsu Kousoku(日月高测) by Nakane Genkei, a famous scholar of the Edo period, as a means of exploring the relevance and different paths of development of the traditional measurement methods in China and Japan.

Key words: Rigao Tu(日高图); the method of double differences; measurement by Gougu; Jitsugetsu Kousoku(日月高测)

南宋以降的比例算法及其渊源——以“异乘同除”为中心

潘澍原

（中国科学院自然科学史研究所）

比例算法是中国古代一种基础而普遍的数学知识，早期算学经典《九章算术》中的“今有术”即其典型，而粟米、衰分、均输诸章多用之。南宋商品经济繁荣，比例算法切近日用，时以“粟米互易（换）”“互换乘除”等称之，在承用“今有术”算法框架的基础上，出现相对具体的计算操作指引。元中叶以后，数学知识主流逐渐向实用化、大众化转变，解题思路更为直接、算法程序更为简易、布算指引更为明晰的“异乘同除”应运而生，成为晚明西学传入以前主要通行的比例算法。细考元明清数学文本所见“异乘同除”的算法、算草及歌诀、图示、注释、解说等材料，同名之下存在着两种不同的数学实作和与之相应的不同理解方式；据此上溯，考察《九章算术》诸章算题施用“今有术”的算法陈述，亦可区分出两种不同的数学实作和理解方式，藉此确证“异乘同除”的古代渊源，即《九章算术》衰分章中所施用的“今有术”。此外，编纂者或将前代典籍的相关算题归入当时通行的某种比例算法名下，或将某种比例算法置于“九章”或“乘除”的著述体系之中，甚或将中国流行的“异乘同除”与欧洲传入的“三率法”关联对应，在表达各自数学理解的同时，亦构成各自对数学知识的历史书写。 

Proportional Algorithms in China Since 13^th Century and Their Epistemic Origins — A Study Centered on “Multiplying by the Different and Dividing by the Same”

PAN Shuyuan

Proportional algorithms were foundational and general mathematical knowledge in ancient China. As the most representative expression, “Suppose procedure” (jinyou shu) was presented in the mathematical classic The Nine Chapters on Mathematical Procedures (jiuzhang suanshu), and was commonly applied in the chapters. From the mid-13th century onward, proportional algorithms gained practical prominence due to the flourishing of the commodity economy in Chinese society. As a result, arithmetical methods with more explicit operational guidelines developed, and the one entitled “multiplying by the different and dividing by the same” (yicheng tongchu) became the dominant method until the introduction of mathematics from Europe in the early 17th century. Interestingly, from algorithms to diagrams, from rhymed prescriptions to annotations, textual materials show that practices differed under the same designation, and suggest that there existed two understanding approaches. Furthermore, two mathematical practices and their underlying understandings in the Nine Chapters, accordingly, may also be distinguished. Thus we could indicate that the “suppose procedure” applied in the 3rd Chapter “sharing according to the degree” (cuifen) of the Nine Chapters is the very epistemic origin from which “multiplying by the different and dividing by the same” derived. In light of this, we will further discuss the historiographical awareness when those proportional algorithms were incorporated in compilations of mathematical texts in the 15-17 centuries China.

中国古代算书与清丈的土地面积计算比较研究

王思琛

土地丈量是中国古代政府运行、政策制定，也是百姓分产、买卖、纳税的重要依据。有效的土地丈量可以调节社会矛盾，维护社会经济政治秩序。中国古代算书中，涉及土地面积计算的部分被称为方田，通常位于算书的开篇第一章，是中国古代算书的重要组成部分。随着数学水平的提高和实际丈量中的需求增多，算书中对于不同图形的面积计算提出了更多更精确的算法。本文将算书中方田章记载的面积算法与实际清丈中的土地测量计算分别进行梳理，辨析二者之间的关系。从算书中的田型名称、清丈中的流程、人员、工具、算法、思想等方面展开讨论，以四不等田、三广田等为案例，展现算书和实际清丈中的异同。揭示了算书的应用性、对清丈的指导性，以及清丈对算学发展的引领性作用。 

Comparative Study on the Calculation of Land Area in Ancient Chinese Mathematics Books and Actual Measurements

WANG Sichen

Land measurement was an important basis for the operation of the ancient Chinese government, the formulation of policies, as well as for the people's division of property, sale and purchase, and payment of taxes. Effective land measurement could regulate social conflicts and maintain socio-economic and political order. In ancient Chinese mathematics books, the part involving the calculation of land area was called “Fangtian”, which was usually located in the first chapter of the mathematics book. With the improvement of mathematical level and the increase of demand in actual measurement, more and more accurate algorithms for the calculation of the area of different shapes are proposed in the mathematics book. In this paper, the area algorithms recorded in “Fangtian” chapter of the book of reckoning and the land measurement calculations in the land measurement are sorted out separately to identify the relationship between the two. It discusses the names of the field types in the mathematics book, the process, personnel, tools, algorithms, and ideas in the land measurement, and takes the “Sibudeng” and “Sanguang” shapes as cases to show the similarities and differences between the mathematics book and the actual measuring of the land. It reveals the applicability of the mathematics book, and the leading role of the land measurement in the development of mathematics.

日本学者林鹤一与中国的学术往来

张晓雪 代 钦

（内蒙古师范大学）

摘要：林鹤一（1873-1935）是日本数学家、数学教育家、数学史家，未曾到过中国，仍与中国学术往来颇深。本文基于原始资料，围绕林鹤一与中国数学家、中国数学教育和中国数学史三方面展开研究。这不仅丰富林鹤一的人物研究、中日数学交流史的内容，更能促进中日数学友好交流和发展。研究发现，作为其学生的中国数学家、数学教育家黄际遇、陈建功、苏步青，在学习和生活上都得到了他及时的帮助；林鹤一与中国数学家华罗庚和中国数学史家李俨的交流,促进了中日数学的友好交流。这些也成为中国更多译介林鹤一著作的主要原因。

关键词：林鹤一，中日数学交流，数学史，数学教育史 

Japanese Scholar Tsuruichi Hayashi’s Academic Exchanges with China

Xiaoxue Zhang and Dai qin

（Inner Mongolia Normal University）

Abstract：Tsuruichi Hayashi is a Japanese mathematician, mathematics educator and mathematical historian. He had never been to China, but had deep academic exchanges with China. Based on original materials, this article focuses on Hayashi and Chinese mathematicians, Chinese mathematics education and Chinese mathematics history. The study found that Chinese mathematician and mathematics educator Huang Jiyu, Chen Kien-kwong and Su Buchin, who were students of Hayashi, had received timely help from Hayashi in their study and life. Hayashi’s exchanges with Chinese mathematician Hua Loo-keng and Chinese historian of mathematics Li Yan, promote the friendly exchanges of mathematics between China and Japan. These are also the main reasons why there were more selections from the writings of Hayashi among translated mathematics books in China.

Keywords： Tsuruichi Hayashi  Mathematics exchanges between China and Japan  History of mathematics  History of mathematics education

中算思想在现代数学教学中的应用初探

汪晓勤

（华东师范大学数学科学学院）

摘 要：中国传统数学历史悠久、博大精深、独具特色，为今日数学教学提供了丰富的素材和思想方法。本报告将从中算文献中总结和提炼出“求同存异”“形诡量均”“类聚群分”“积微成著”“殊途同归”等思想，并探讨这些思想在现代中学数学中的广泛应用，试图证明：运用中算思想，不仅可以解决形形色色的代数、几何、三角、解析几何问题，还可以将今日数学课程中散落在不同领域、不同主题背后的思想方法统一起来，从而展示中华有优秀传统数学文化的迷人魅力、中算素材的巨大价值和古为今用、推陈出新的精彩实例。作为创新之源的中算史，为中华优秀传统文化何以优秀提供了注解。

关键词：中算思想；古为今用；创新；数学教学

Preliminary Exploration of the Application of Ancient Chinese Mathematical Thought in Modern Mathematics Teaching

WANG Xiaoqin

Abstract: Traditional Chinese mathematics, with its long history, profound depth, and distinctive characteristics, offers abundant materials and methodological insights for contemporary mathematics education. This report summarizes and extracts key principles from classical Chinese mathematical texts, such as "seeking common ground while preserving differences" (求同存异), "unconventional forms with equal quantities" (形诡量均), "categorization and classification" (类聚群分), "accumulating subtleties to achieve significance" (积微成著), and "different paths leading to the same destination" (殊途同归). It further explores the extensive applications of these principles in modern secondary school mathematics teaching, demonstrating that employing traditional Chinese mathematical thinking can not only solve diverse problems in algebra, geometry, trigonometry, and analytic geometry but also unify the underlying methodologies scattered across different fields and topics in today's mathematics curriculum. Through this, the report highlights the captivating charm of China's outstanding traditional mathematical culture, the immense value of classical Chinese mathematical materials, and provides wonderful examples of adapting ancient wisdom for modern use and innovation. As a source of creativity, the history of Chinese mathematics offers a compelling explanation for why China's traditional culture remains exceptional.

Keywords：Key Principles of Traditional Chinese Mathematics; Adaptation of Ancient Wisdom for Modern Use; Innovation；Mathematics Teaching

“中国三角形数”的历史文化价值和教育功能

代钦

内蒙古师范大学科学技术史研究院

摘  要：“毕达哥拉斯三角形数”在西方数学文化中具有独创性的象征意义，也是西方数学文化的符号。我们在以往的中外数学史和数学文化教育中一直如是叙说的。然而，考古发现有力地证实了中国人在五千年前的新石器时代陶器上已经创造了这种“三角形数”，本文把它叫做“中国三角形数”。中国新石器半坡文化母体中孕育数学文化的基因——“中国三角形数”以来，便在神州大地生根发芽，开花结果。“中国三角形数”在汉代以来的《九章算术》《杨辉算法》《算学宝鉴》等数学典籍以及艺术作品中一脉相承地延续发展，已经成为中华优秀数学文化的有机组成部分。“中国三角形数”在中小学数学教学中具有极为重要的作用：一是为中小学数学教学中融入中华优秀数学文化，进行民族自信心和自尊心教育提供了珍贵文献；二是为中小学数学教学中渗透中国传统数学思想方法提供了有益素材。

关键词：中国三角形数，新石器时代陶器，中国数学典籍，中小学数学教学，文化价值和教育功能

Historical and Cultural Value and Educational Function of “Chinese Triangle Number”

Qin Dai

Institute for the History of Science and Technology, Inner Mongolia Normal University

Abstract: “The Pythagorean triangle number” has unique symbolic significance in Western mathematical culture and is also a symbol of Western mathematical culture. We have always said this in the history and cultural education of mathematics both domestically and internationally. However, the archaeological discoveries strongly confirmed that the Chinese had created this “triangle number” on Neolithic pottery five thousand years ago, which is called “Chinese triangle number” in this paper. Since the birth of the mathematical culture gene “Chinese Triangle Number” in the mother body of the Neolithic Banpo culture in China, it has taken root, sprouted, blossomed, and borne fruit on the land of China. The concept of “Chinese triangle numbers” has been continuously developed in mathematical classics and art works such as Nine Chapters on Mathematical Art （《九章算术》）, Yang Hui Algorithm （《杨辉算法》）, and Mathematical Encyclopedia （《算学宝鉴》） since the Han Dynasty, and has become an organic part of China’s excellent mathematical culture. The “Chinese Triangle Number” plays an extremely important role in mathematics teaching in primary and secondary schools. Firstly, it provides valuable literature for integrating excellent Chinese mathematical culture into mathematics teaching in primary and secondary schools, and promoting national confidence and self-esteem education; Secondly, it provides useful materials for the infiltration of traditional Chinese mathematical thinking and methods in primary and secondary school mathematics teaching.

Key words: Chinese Triangle Number，Neolithic pottery，Chinese Mathematical Classics，Mathematics Teaching in Primary and Secondary Schools，Cultural Value and Educational Function

关于传统历法历经的标点分段方法刍论

王荣彬

(内蒙古师范大学；中国民主同盟中央委员会)

摘  要  一部历经即为一部历法的算法集，而中国古代历法的算法，从汉代《太初历》到元代《授时历》皆为筹算传统，且与中国古代数学的筹算传统一致。在二十四史中，有十六史包含律历志或历志（合称历志），其中完整收录了39部历法的历经。中华书局点校本对这些历志及其历经进行了标点和分段，由于各史的历志点校工作出自不同专家之手，加之当时对历志这种专门文献标点分段问题的特殊性没有专门研究，且没有统一规范协调，致使其历志及其历经的标点和分段问题相对更加突出。本文关注在读懂原文而句读不误前提下，对如何准确地用新式标点符号再现历经原文的语义、语气、情态、结构层次等进行了专门讨论。根据筹算系统特有的布算方法机械化、程序化的鲜明特色，历法算法的推算过程及其中的程序链和逻辑链，以及其文字表述的特点，提出了一些相应的标点和分段方法的约定。以抛砖引玉，并希望约定俗成。

关键词  传统历法，历经，文献整理，标点，分段

A Preliminary Discussion on Punctuation and Paragraphing Methods for Traditional Calendar Classics

Wang Rongbin
Inner Mongolia Normal University; Central Committee of China Democratic League

Abstract: A calendar classic (历经) constitutes a collection of algorithms for calendrical systems. The computational methodologies of ancient Chinese calendars, from the Taichu Calendar (太初历) of the Han Dynasty to the Shoushi Calendar (授时历) of the Yuan Dynasty, were rooted in the rod-based computational tradition, consistent with the mathematical practices of ancient China. Among the Twenty-Four Histories (二十四史), sixteen include "Treatises on Harmonics and Calendrics" (collectively termed lizhi 历志), which preserve 39 complete calendar classics. While the punctuated and collated editions published by Zhonghua Book Company (中华书局) have standardized these treatises, inconsistencies in punctuation and paragraphing persist due to variations in expertise among scholars involved in the editorial process, the absence of specialized studies on the unique challenges of punctuating calendrical texts, and the lack of unified guidelines. This paper focuses on accurately rendering the semantic meaning, tone, contextual nuance, and structural hierarchy of calendar classics using modern punctuation, under the premise of faithful textual comprehension. By analyzing the mechanical and procedural characteristics of rod-based computation, the logical and procedural chains in calendrical algorithms, and the stylistic features of classical texts, this study proposes a series of conventions for punctuation and paragraphing. It aims to initiate scholarly dialogue and foster consensus in this specialized field.

Keywords: Traditional calendars, calendar classics, textual collation, punctuation, paragraphing

从《九章算术》的“勾股容圆”到和算的“容题”———东亚代数化几何的源流与意义

徐泽林

东华大学人文学院，上海，200051

张建伟

天津师范大学教育学部，天津，300387

摘要：一般认为，中国传统数学中代数学发达，几何学不发达，这种认识是以希腊演绎几何为评价标准。作为古典几何学的综合几何，并非仅有演绎几何一种类型，中国传统数学中也并非仅有度量几何，还包括为列代数方程服务的几何内容，这种几何利用图形结构及其性质建立代数关系，以列代数方程，为解方程服务，吴文俊将这种几何概括为“代数化几何”。代数化几何学发端于《九章算术》的“勾股章”，其中一些问题通过“出入相补”的等积变换来探索几何量的代数关系，以推演带从开方式（一元二次方程），这种方法在宋元时期演变为“条段法”，随着天元术的发明与应用，代数化几何成为宋元数学的主流内容。宋元代数化几何具有以下几方面特征：

第一：这类几何并非是用来解决实际问题，而是用来进行纯代数分析。它往往处理不同维度几何量间的运算问题，这是没有实际应用背景的，纯粹是为了获得高次方程而构造的代数关系。

第二：这类几何伴随代数演算方法的进步而发展，从古代的“出入相补”到宋元的条段法，再到天元术与四元术，这些代数演算都是所谓的演段。宋元时期的代数化几何都与天元术密切相关。

第三：几何图形模型化。出现了勾股形、“圆城图式”等几何模型，虽对几何图形性质有认知，但不注意其表述，更不关心几何性质间的逻辑关系，而是利用几何性质构建代数关系。

由于天元术在明代中国失传，代数化几何传统在中国传统数学中也随之消亡。然而，它随《算学启蒙》在江户日本的传播与影响，在和算中获得高度发展，内容不断丰富，成就斐然，成为和算的一大特色。

和算家建部贤弘（1664～1739）等人在《大成算经》（1711）明确将数学问题处理的对象分为“象”与“形”对立的两大类，即把数学研究对象区分为非几何与几何两大类，其卷10至卷15专门讨论几何图形的计算问题，首次对几何图形问题进行分类，将其分为：

（1）形法：即各类图形的计算公式，包括方法（正方形计算方法）、直法（长方形计算方法）、勾股法（直角三角形计算方法）、斜法（一般三角形计算方法）、角法（正多边形计算方法）等；

（2）形率：即几何度量计算中所用的常数，如圆率（圆周率）、弧率（弧长计算中的常数）、立圆率（球体积计算中的常数）、球闕率（球冠体积计算中的常数）等曲线曲面体计算公式（带有常数）；

（3）求积：平积（平面图形面积）、立积（立体图形体积），即面积与体积的度量计算；

（4）形巧：截术（分割图形）、接术（拼接图形）、容术（容切图形）、载术（一侧与直线相切的几何图形）、绕术（曲线缠绕图形）等，各种复杂几何图形的计算。

上述分类建立起几何知识框架，为几何图形分析在和算中发展开拓了广阔空间。其中首次将“容题”列为一类几何问题。在中日代数化几何问题中，“容题”是一类极为典型和普遍的几何图形，普遍存在于中日算书之中，在代数化几何发展史上发挥了重要作用。

所谓“容题”，和算家有时称作“容术”，指三角形、多边形、圆、椭圆等图形之间内外切、内外接而构成的几何图形。它起源于中国《九章算术》的“勾股容方”“勾股容圆”以及李冶的“圆城图式”等几何模型，江户初期的《算法根源记》（1666）《古今算法记》（1671）《发微算法》（1674）等遗题承继的系列算书中，开始大量出现。《大成算经》之后，有马赖徸（1714～1783）的《拾玑算法》（1769）卷二专设“容题”一节，专门讨论容题图形的计算。

随该书对关流旁书法、演段术的传播，代数化几何在和算中获得长足发展，至幕末，和算容题日益丰富，包括勾股容方（圆、直、三边形、多边形、菱、侧圆），以及団扇容题。“容题”在和算中的流行，从一个侧面反映出代数化几何在江户日本的发达。以“容题”为代表的东亚代数化几何，与笛卡尔解析几何有异曲同工之处，和算几何成就可以与19世纪西方的综合几何相媲美。

关键词：勾股容圆;容题;代数化几何;综合几何

From "Gougu Rongyuan(勾股容圆)" in Nine Chapters on the Mathematical Art to "Yodai(容题)" in Wasan: The Origins and Significance of Algebraized Geometry in East Asia

 XU Zelin

College of Humanities, Donghua University, Shanghai 200051, China

ZHANG Jianwei

Faculty of Education , Tianjin Normal University, Tianjin 300387, China

Abstract: It is generally believed that traditional Chinese mathematics was advanced in algebra but underdeveloped in geometry.This view is based on the standards of Greek deductive geometry.

However, synthetic geometry, as a classical form, is not limited to deductive geometry alone, and Traditional Chinese mathematics includes not only metric geometry but also geometric content designed to serve the construction of algebraic equations. This geometry uses the structure and properties of geometric figures to establish algebraic relationships and form algebraic equations, ultimately serving to solve these equations. Wu Wenjun summarized this type of geometry as "algebraized geometry."

Algebraized geometry originated in the "Gougu Chapter（勾股章）" of the Nine Chapters on the Mathematical Art, where some problems explored the algebraic relationships of geometric quantities through equal-area transformations, such as the "Out-in Complementary Principle." This led to the derivation of Daizong kaifang shi (带从开方式，the method of solving quadratic equations).This method evolved into the Tiaoduan-fa（条段法）during the Song and Yuan dynasties, and with the invention and application of the Tianyuan（天元术）, algebraized geometry became a central feature of Song and Yuan mathematics. Algebraized geometry in the Song and Yuan periods had the following characteristics:

Firstly: This type of geometry is not used to solve practical problems, but rather for pure algebraic analysis. It often deals with operations between geometric quantities of different dimensions, with no practical application background. It is purely constructed to derive algebraic relations for obtaining higher-degree equations.

Secondly: This type of geometry developed alongside the advancement of algebraic calculation methods, from the ancient "Out-in Complementary Principle" to the Tiaoduan-fa（条段法） in the Song and Yuan dynasties, and then to the Tianyuan shu（天元术） and Siyuan shu（四元术）. These algebraic calculations are known as " Yanduan（演段）" Algebraized geometry in the Song and Yuan periods was closely tied to the Tianyuan shu（天元术）.

Thirdly: Geometric modeling. Geometric models such as the Gougu（勾股） and Yuancheng tushi（圆城图式）emerged. While there was an understanding of the properties of geometric figures, there was little focus on their formal representation, nor was there concern for the logical relationships between geometric properties. Instead, geometric properties were used to construct algebraic relationships.

Due to the loss of the Tianyuan shu in Ming-dynasty China, the tradition of algebraized geometry also disappeared from traditional Chinese mathematics. However, through the dissemination and influence of Suanxue Qimeng（算学启蒙） in Edo-period Japan, it was revived and further developed within Wasan. The content of algebraized geometry in Wasan became increasingly enriched, yielding remarkable achievements and establishing it as a distinctive feature of Japanese mathematics.

Wasan mathematicians Takebe Katahiro (建部賢弘，1664–1739) and others, in the Taisei Sankei (大成算経，1711), clearly divided mathematical problems into two opposing categories: Xiang（象） and Xing（形） , thereby distinguishing between non-geometrical and geometrical types of mathematical inquiry. Volumes 10 through 15 of the work are dedicated to the calculation of geometrical figures, and for the first time, geometrical problems were systematically categorized as follows:

 (1) Keihō(形法，Shape Method): This refers to the computational formulas for various geometric figures, including methods such as: Hōhō(方法，method for calculating squares, Chokuhō(直法，method for calculating rectangle), Kōkohō(勾股法，method for calculating right triangles, Shahō (斜法，method for general triangles, Kakuhō (角法，method for regular polygons), and so on.

 (2)Keiritsu(形率，Shape Ratio) :This refers to the constants used in geometrical measurement calculations, such as Enritsu (圓率,circle ratio or π), Koritsu(弧率，arc ratio, a constant used in arc length calculations), Ritsuenritsu(立圓率，solid circle ratio, used in sphere volume calculations), and Kyūketsuritsu(球闕率，spherical segment ratio, used in spherical cap volume calculations). These are formulas for calculating curved surfaces and solids that involve constants.

 (3) Kyūseki (求積，Area/Volume Calculation): This includes Heiseki(平積，calculation of the area of plane figures) and Ritsuseki (立積，calculation of the volume of solid figures), referring to the measurement and computation of area and volume.

 (4)Keikō(形巧，Geometrical Ingenuity): This includes various methods for handling complex geometric figures, such as Setsujutsu (截術，sectioning of figures), Setsujutsu (接術，joining of figures), Yōjutsu (容術，containment or tangency of shapes), Saijutsu (載術，figures tangent to a line on one side), and Ryōjutsu (繞術，figures involving curved encirclement).

The above classification established a framework for geometric knowledge and opened up vast space for the development of geometric figure analysis in Wasan. For the first time, it classified Yōdai(容題，containment problems as a distinct type of geometric problem. In both Chinese and Japanese algebraized geometry, Yōdai are a very typical and common type of geometric figure, widely present in mathematical texts from both China and Japan, and have played an important role in the history of algebraized geometry development.

Sometimes, Wasan mathematicians also refer to Yōdai as Yōjutsu(容術), which refer to geometric figures formed by inscribing and circumscribing triangles, polygons, circles, ellipses, and other shapes.It originated from the geometric models such as Gougu rongfang(勾股容方) and Gougu rongyuan(勾股容圆) in the Nine Chapters on the Mathematical Art, as well as Li Ye's(李冶) Yuancheng tushi(圆城图式). These concepts began to appear frequently in a series of mathematical texts inherited from earlier works such as Sanpō Kongengi (算法根源記，1666), Kokon Sanpōki (古今算法記，1671), and Hatsubi Sanpō (発微算法，1674) during the early Edo period. After Taisei Sankei, Arima Yoriyuki (有馬頼徸，1714–1783) dedicated an entire section to Yōdai(容題) in Volume 2 of Shuuki Sanpō (拾璣算法,1769), where he specifically discussed the computation of Yōdai.

With the dissemination of the Hōshohō(旁書法，marginal annotation method) and Endanjutsu(演段術，an algebraic method of calculating the coefficient of polynomial with the polynomial as its center) from the school of Seki Takakazu(関孝和) through this book, algebraized geometry saw significant development in Wasan(traditional Japanese mathematics).By the end of the Edo period, Yōdai in wasan had become increasingly diverse, including Gougu rongfang (勾股容方，such as circles, straight lines, triangles, polygons, rhombuses, and circumscribed circles), as well as Dansen Yōdai (団扇容題，the Fan-shaped Containment Problem ). The popularity of Yōdai in wasan reflects, from one perspective, the development of algebraized geometry in Edo-period Japan.The East Asian algebraized geometry, represented by Yōdai shares similarities with Descartes' analytical geometry, and the achievements of Wasan geometry can be compared to 19th-century Western synthetic geometry.

Keywords: Gougu rongyuan(勾股容圆,Incircle of a Right-Angled Triangle), Yodai(容题, Tangent-containing embedded graph), algebraized geometry, synthetic geometry.

21世纪国际数学基础教育标准变化趋势——以中国和英国为例

潘钺

（中国科学技术大学科技史与科技考古系，安徽 合肥 230026）

摘要：基于对中国《义务教育数学课程标准（2022年版）》（以下简称“新课标”）和英国最新小学数学国家课程（Key Stage 1&2）的比较研究，探讨了21世纪国际数学基础教育课程标准的演变趋势，聚焦课程结构、核心素养培养和教学方法三大维度。两国课程标准均体现出从知识本位向核心素养导向转变的趋势，都强调培养学生的数学思维能力和问题解决能力。在课程结构方面，新课标包含数与代数、图形与几何、统计与概率和综合与实践四个领域，特别强化了综合与实践板块，通过主题式和项目式学习促进跨学科知识应用。英国课程按照关键阶段和年级列出各数学领域的学习目标，但同时鼓励学生在不同数学主题之间建立联系并将所学应用于现实情境。在核心素养培养方面，新课标首次明确了包含数感、符号意识、模型意识等在内的11项数学核心素养，英国课程未列出细目而是以“流畅性、推理、解决问题”三大目标贯穿始终。教学方法上，新课标倡导单元整体教学设计和“因材施教”，鼓励通过探究、项目学习等多样化方式培养素养；英国则普遍推行“数学掌握”教学法，采取全班统一进度、深度理解优先的模式，利用高质量教材和丰富练习确保大多数学生打好基础。总体而言，中英两国课程标准的改革都反映出面向21世纪培养数学关键能力的共同趋势，但实现路径各有侧重。跨国比较带来的启示是，应平衡基础知识传授与核心能力培养，在未来课程标准发展中互鉴融合各国优势，以更好地应对未来教育挑战。

关键词：数学课程标准，核心素养，课程改革，国际比较，基础教育

21st-Century Trends in International Mathematics Curriculum Standards: A Comparative Study of China and the UK

PAN Yue

Abstract: This study examines the evolving trends of 21st-century international mathematics curriculum standards in basic education by comparing China’s 2022 compulsory mathematics curriculum standard with British latest primary mathematics national curriculum (Key Stages 1 and 2). The comparison focuses on three dimensions: curriculum structure, cultivation of core competencies, and teaching approaches. The analysis reveals that both countries’ standards are shifting from a purely knowledge-based orientation toward a competency-driven model. Both emphasize the development of students’ mathematical thinking and problem-solving skills as key outcomes. In terms of curriculum structure, China’s 2022 standard is organized into four content domains (Number & Algebra, Geometry, Statistics & Probability, and Integrated Practice), with a dedicated Integrated Practice component that elevates applied, project-based learning and cross-disciplinary themes to solve real-world problems. British national curriculum is structured by key stages and year-by-year objectives across mathematical domains, but it similarly encourages rich connections across different topics and applying knowledge in real contexts Regarding core competencies, the Chinese curriculum explicitly outlines 11 mathematical core literacy components – including number sense, symbolic awareness, modeling thinking, etc. – reflecting a formal incorporation of “mathematical core competencies” into standards. The English curriculum does not enumerate specific competencies in this way; instead, it embeds similar ideas in three overarching aims: fluency, reasoning, and problem-solving. Concerning pedagogical approaches, China’s new standard advocates holistic unit planning and differentiated instruction, encouraging exploratory learning and project work to foster students’ competencies. In contrast, Britain has implemented a widespread “mathematics mastery” approach, characterized by whole-class progression and depth-before-speed learning, supported by high-quality textbooks and varied practice, to ensure a solid foundation for the majority of pupils. In conclusion, both countries’ reforms reflect a common direction toward enhancing students’ mathematical literacy and skills for the 21st century, albeit via different strategies. The cross-national comparison provides insights that balancing fundamental knowledge and key competencies is essential; future curriculum development should incorporate the strengths of each system, fostering an internationally-informed approach to improving mathematics education.

Key words: mathematics curriculum standards, core competencies, curriculum reform, international comparison, basic education

古为今用 立德树人——中算史在二元一次方程组单元教学中的应用

邹佳晨 汪晓勤

（华东师范大学教师教育学院，上海 200241）

摘 要：中国传统数学有着悠久的历史、辉煌的成就和丰富的内容，中算史既是数学教学的目标，也是数学教学的工具，应当发挥更大的教育价值。本文以初中数学二元一次方程组单元教学为例，融入中算史中的二元问题，按照“古名今辩”“古题今解”“古术今推”“古法今用”“古问今编”“古算今思”6种策略设计教学留白创造式教学，教师在课堂上留陈述之白、方法之白、论证之白、发现之白、问题之白和超越之白，体现数学课堂的德育价值。

关键词：中算史，二元一次方程组，单元教学Using History to Teach Mathematics for Moral Education and Talent Development——Application of Chinese traditional mathematics in unit-based instruction on systems of linear equations in two variables

Zou Jiachen, Wang Xiaoqin

Abstract: Chinese traditional mathematics boasts a profound history, illustrious achievements, and rich content. The history of Chinese mathematics serves not only as an objective of mathematics education but also as a pedagogical tool, whose educational value should be further harnessed. This study explores unit-based instruction on systems of linear equations in two variables in junior high school mathematics by integrating binary problems in the history of Chinese mathematics. Guided by the Chinese inquiry-based teaching(留白创造式教学), we design instructional activities using six strategies: interpreting ancient terms through modern lenses (古名今辩), solving classical problems with contemporary methods (古题今解), deducing historical algorithms via modern reasoning (古术今推), applying ancient techniques to current contexts (古法今用), reconstructing historical questions for modern inquiry (古问今编), and reflecting on ancient mathematics with critical perspectives (古算今思). By embedding gap leavings in teaching, including gaps of statements, methodologies, reasoning, discoveries, questions, and transcendence, teachers can leverage the moral education value of mathematics classrooms.

Keywords: history of Chinese mathematics; systems of linear equations in two variables; unit-based instruction

A Study on the Calculation and Accuracy of Solar Eclipse in Tibetan Shixian System(rgya rtsis)

GUO Tian

(Institute for Advanced Study in History of Science, Northwest University, Xi'an 710127,China)

Abstract  The Shixian Calendar (時憲歷,1645) of the Qing dynasty is a calendrical system that integrates traditional Chinese mathematical astronomy with Western astronomy. During the 18th century, it was introduced into the Tibetan regions through two transmissions channels: One is the emperor Kangxi-sponsored official translation version—rgya rtsis chen mo (康熙御制漢曆大全藏文譯本,1715), the other is locally compiled Tibetan version of the Shixian Calendar. This study focuses on the solar eclipse algorithms found in both versions, offering a comparative analysis of their textual sources, numerical tables, and astronomical models. The eclipse algorithms in the official translation version is derived directly from the Suan Qizheng Jiaoshi Lingfan Fa  (算七政交食凌犯法,1694), which is translated almost verbatim. By comparing the eclipse algorithms in the rgya rtsis snying bsdus(马杨漢曆心要,1744) and the rgya rtsis 'jm dbyng dgyes pa'i mchod sprin (汉历文殊喜悦供云,1987), which are the foundational text and the latest version of the Tibetan Shixian System (rgya rtsis) respectively, it can be observed that the eclipse limit values and solar motion tables are derived from the Yuzhi Lixiang Kaocheng Houbian(御制历象考成后编，1742), while the remaining numerical tables are sourced from the Yuzhi Lixiang Kaocheng Biao (御制历象考成表，1732). The main content of the eclipse algorithm and its astronomical model are based on the Yuzhi Lixiang Kaocheng (御制历象考成，1724). Therefore, the Tibetan Shixian System may be regarded as an adaptation and assimilation of the Lixiang Kaocheng series produced during the Qing dynasty. To further evaluate the computational accuracy of this calendrical system, this study uses a Python program to simulate the times of three phase of solar eclipses for the period between 1744 and 1844. The results are compared with the data extracted from the SkyMap software. The average errors for eclipse maximum, first contact, and last contact are found to be 40.22, 45.27, and 40.72 minutes, respectively, mean error of the magnitude of the eclipse is 0.12. In terms of computational precision, this system outperforms the Tibetan Kālacakra System in the same period, though it remains slightly less accurate than the original Qing dynasty Shixian system. 

Key words   Tibetan ShiXian System, Solar eclipse, Accuracy of the Algorithms,  rgya rtsis snying bsdus

The First/Last Visibility of Planets in Ancient Astronomy: Babylon, Greece, Arabia, India, and China

王振华

（西北大学）

摘要：第一次和最后一次见的预测与计算在古代文明的行星观测与历法编制中反复出现，但不同文明对此天象的理解与处理方式存在显著差异。本研究以太阳系五大行星（金星、木星、水星、火星与土星）的“第一次和最后一次见”作为研究对象，系统梳理和比较了古代巴比伦、希腊、阿拉伯、印度和中国文明在这一领域的历史文献与计算方法。通过跨文化的文献研究与理论比照发现，尽管第一次和最后一次见作为会合周期的重要特征广泛出现在各文明的天文学文献中，但仅古代巴比伦将其视为重要观测现象，然而缺乏明确的判断规则；古希腊和阿拉伯文明受几何学模型影响，将这一现象从行星位置计算中分离，精细地考虑了地理纬度、季节和行星黄纬；而古印度和中国则基于代数传统，将其简单视为行星位置计算中的一种特殊节点，通常忽略了行星黄纬。然而，除古代巴比伦外均以太阳与行星的黄道距角或赤道距角判断其可见性。进一步基于现代天文学理论的模拟与验证结果显示，使用距角方法预测行星可见性时，观测季节和地理纬度的影响至关重要。这一方法虽不够精准，但因其便于操作且直观，能够满足古代天文学家无需精确推算实际天象的实际需求。本研究揭示了古代文明在天文观测与计算技术演进中的相似与差异，深化了对古代天文学发展的理解，同时也为现代天文学史与科学史研究提供了重要的比较视角与理论参照。

Abstract: The prediction and calculation of the first/last visibility of planets frequently appeared in the astronomical observations and calendar compilations of ancient civilizations, though there were notable differences in how each civilization understood and managed these celestial events. Taking the first/last visibility of the five classical planets (Venus, Jupiter, Mercury, Mars, and Saturn) as the subject of investigation, this study systematically reviews and compares historical records and computational approaches from ancient Babylonian, Greek, Arabic, Indian, and Chinese traditions. Cross-cultural analysis of historical texts and theoretical methods reveals that while these visibility phenomena were widely acknowledged as significant points within planetary synodic cycles across all examined civilizations, only the Babylonians attributed special observational significance to them without providing clear criterion for judgement. The Greek and Arabic astronomical traditions, influenced by geometric models, treated the phenomena separately from planetary positional calculations, meticulously incorporating geographic latitude, seasonality, and planetary ecliptic latitude into their methods. In contrast, ancient Indian and Chinese traditions, rooted in algebraic calculation, merely considered these events as special nodes within broader planetary computations, typically neglecting planetary ecliptic latitude. Nevertheless, aside from the Babylonians, all these

中算下南洋：马新华人学者的中国数学史研究

应成霞

（上海交通大学 科学史与科学文化研究院，上海 200240）

摘  要：伴随着人口的流动和文化的传播，中国传统数学研究汇集于马来西亚和新加坡，可谓中算下南洋。马新华人学者的中国数学史研究是主要动力，以何丙郁、蓝丽蓉和洪天赐师徒三人为主。本文聚焦于他们成长教育环境的背景、进入中算研究的源流、立志研究事业的学术，从中考察中算的南洋之旅，探讨南洋地区的中算研究。其中李约瑟是重要的媒介，他把何丙郁引向数理天文，但把蓝丽蓉引入数学史，又由何丙郁把蓝丽蓉和洪天赐带入数学史。何丙郁对中国科学史的研究起于中国数学史的研究，蓝丽蓉至始至终专研中国传统数学，洪天赐以中华文化视角探讨中国古代数学，通过他们的诠释使海外领略了中国传统数学的魅力。

关键词：中国数学史；南洋；华人学者；李约瑟

Chinese Mathematics Went to Nanyang: A Study of the History of Chinese Mathematics by Malaysian-Singaporean Scholars of Chinese Descent

YING Cheng-xia

(School of History and Culture of Science, Shanghai Jiao Tong University, Shanghai 200240, China)

Abstract With the flow of population and the spread of culture, study on traditional Chinese mathematics is gathered in Malaysia and Singapore, i.e. Chinese mathematics went to Nanyang. The group of Malaysian-Singaporean scholars of Chinese descent is the main driving force of the research on the history of Chinese mathematics, mainly composed of Ho Peng Yoke, Lam Lay Yong and Ang Tian Se. This paper focuses on the background of their growth and educational environment, the origin of entering the Chinese mathematics research, the academics of their aspiring research career, and examines the journey of Chinese mathematics research in Nanyang and discusses the Chinese mathematics research in Nanyang. Joseph Needham is an important medium throughout, who led Ho Peng Yoke into the mathematical astronomy, introduced Lam Lay Yong to the history of mathematics. After that, owing to Ho’s efforts, Lam Lay Yong and Ang Tian Se entered the history of mathematics. Ho Peng Yoke’s research on the history of Chinese science started from the study of the history of Chinese mathematics, Lam Lay Yong studied traditional Chinese mathematics all her life, and Ang Tian Se explored ancient Chinese mathematics from the perspective of Chinese culture. Through their interpretation, the overseas people come to understand the charm of traditional Chinese mathematics.

Keywords History of Chinese Mathematics, Nanyang, Scholars of Chinese Descent, Joseph Needham

《南村辍耕录》中的历法歌诀研究

赵蕊

（上海交通大学，上海 200240）

摘  要  元末陶宗仪所著《南村辍耕录》是一部百科全书式的文人笔记，记录宋元时期社会生活，为后人留下了考察当时社会的珍贵史料。卷五的《授时历法》中以歌诀形式呈现历法，尤以《授时历要法歌》为主。本文逐句解读《授时历要法歌，将歌诀按主题分段，重点讨论歌诀中的定年法和定节气法，并结合其他来源的历法歌诀进行分析。利用授时历颁行前后一百年的数据，对《授时历要法歌》中定年法和定节气法的可信性进行验证，得到了较高的准确度，否定了《授时历要法歌》与《授时历》的强关联性。《南村辍耕录》虽为元代笔记，却保留宋朝天文资料，影响明清类书和笔记的编纂。

关键词  《南村辍耕录》，历法歌诀，民间历法，授时历

Research on the Calendar Rhymes in the Nancun Chuogenglu

ZHAO Rui,

（Shanghai Jiao Tong University，Shanghai，200240）

Abstract  The Nancun Chuogenglu, a comprehensive encyclopedia compiled by Tao Zongyi at the end of the Yuan Dynasty, is a scholarly notebook that records social life in the Song and Yuan periods, leaving valuable historical materials for future generations to study the society of that time. Chapter 5 of the book, The Calendar System of Shoushi, presents the calendar system in the form of rhymes, with the Essential Principles of the Shoushi Calendar being the main focus. This article interprets the Essential Principles of the Shoushi Calendar verse by verse, dividing the verses by theme, and focuses on the methods of determining the year and the solar term in the verse. It also analyzes the calendar rhyme from other sources. Using data from the 100 years before and after the promulgation of the Shouxidai Calendar, the article verifies the credibility of the methods of determining the year and the solar term in the Essential Principles of the Shouxi Calendar and obtains a high degree of accuracy, thereby negating the strong correlation between the Essential Principles of the Shoushi Calendar and The Calendar System of Shoushi. Although the Nancun Chuogenglu is a Yuan Dynasty notebook, it preserves the astronomical data of the Song Dynasty and influences the compilation of classics and notebooks in the Ming and Qing dynasties.

Keywords  Nancun Chuogenglu, Essential Principles of the Calendar, Folk calendar, The Calendar System of Shoushi

16世纪中西音乐体系变革背后的数学思想渊源探析

樊宇轩

摘要：1584年中国学者朱载堉于《律历融通》中首次提出十二平均律（或称新法密律），利用弦长的等比测算，彻底解决了困扰中国律学研究道路上难越的关山之险。其运用古代传统方圆术构建了以√2为基础的等比数列，并通过传统工具算盘完成了对√(12&2)的计算并将结果精确到小数点后25位。                    

与之对应1580年西蒙·斯蒂文在其著作中通过“整数化处理”方法得出三个关键音程的近似整数，再以“三项比例法”推导其余 9 个音程的整数弦长，从而得出十二平均律数值。但由于其手稿直至1884年才被人公布，因此在16世纪并未引起较大影响。随后1636年马林·梅森在《普遍和谐》一书中分别介绍了由让·伯格朗、梅尔·布里奥以及让·加莱计算得出的十二平均律表（相比与斯蒂文数值更精确）。本研究通过对比朱载堉与斯特文以及梅森等人计算十二平均律采用算法的异同，揭示中西在16世纪如何分别实现平均律的数学建构，并进一步探讨17世纪梅森对欧洲调律实践的推动作用。

关键词 十二平均律；方圆术；三项比例法

Tracing the Origins of Mathematical Thinking behind the Transformation of Chinese and Western Musical Systems in the Sixteenth Century

Fan Yuxuan

Abstract：In 1584, the Chinese scholar Zhu Zaiyu first formulated the system of twelve‐tone equal temperament (also called the “new method of tuning”) in his treatise Lülirongtong (The Integration of Pitch Systems and Calendrical Astronomy). By constructing a geometric progression based on string lengths and employing traditional Chinese “square‐and‐circle” methods, he calculated the twelfth root of two with an abacus, achieving numerical precision to 25 decimal places. In parallel, in 1580 Simon Stevin in the West employed an “integer‐based” approach to derive approximate integer values for three principal intervals and then used the “rule of three” to determine the remaining nine intervals, thereby obtaining a numerical approximation of twelve‐tone equal temperament. However, Stevin’s manuscript remained unpublished until 1884 and thus exerted little contemporary influence. Later, in 1636, Marin Mersenne’s Harmonie Universelle presented more accurate equal‐temperament tables computed by Jean Beaugrand, Ismaël Boulliaud, and Jean Gallée. This study compares and contrasts the algorithms employed by Zhu Zaiyu, Simon Stevin, and Marin Mersenne in their construction of equal temperament, illuminating how Chinese and European scholars each achieved the mathematical realization of equal temperament in the sixteenth century, and examines Mersenne’s seventeenth-century role in promoting its standardized adoption in Europe.

Keywords: Twelve-tone equal temperament;Geometric methods using squares and circles;Rule of three

用西洋算法解《九章算术》—— 罗士琳《比例汇通》研究

陆忆诚

摘要 罗士琳是清中期重要数学家之一，《比例汇通》是其攥写的第一部数学著作。此书写作的主要目的是说明“《九章》即比例”。其头两卷将《九章算术》归于十二种三率比例法之下，说明“比例通而《九章》无不通”。后两卷则用借方根比例法再次推演，说明借根方是“比例之大全”“可徵《九章》”。《比例汇通》一书以西洋算法重写《九章》，呈现出“西学为法，中学为体”的态势。它的写作是清代数学家试图汇通中西算学的一次重要尝试。书中所展示出的对西法的倡导倾向与罗士琳中后期文章中的观点产生了鲜明的对比，对于理解清代数学家对西学的态度转变有一定意义。

关键词 罗士琳；《比例汇通》；《九章算术》； 

Using Western Algorithm to Rewrite Jiu Zhang Suan Shu

— A Study of Luo Shilin’s Bi Li Hui Tong

Lu Yicheng

Abstract Luo Shilin was an important mathematician in the mid-Qing period, and Bi Li Hui Tong was his earliest mathematical work. The main purpose of this book was to demonstrate that "Jiu Zhang is of proportional algorithms." In its first two volumes, Luo reorganized Jiu Zhang by using twelve types of proportional algorithms, aiming to show that "if one can master proportional algorithms, one can master Jiu Zhang." The latter two volumes rederive these algorithms one by one using a method called "Jie Gen Fang", illustrating that Jie Gen Fang represents the "complete system of proportions" and "can serve as the core of Jiu Zhang". Luo rewrites the Chinese traditional mathematical book using Western algorithms, reflecting a trend of  "Western Learning as Method, Chinese Learning as Substance". Its writing stands as an important attempt by Qing dynasty mathematicians to integrate Chinese and Western mathematical traditions. The book's promotion of Western methods forms a striking contrast with Luo Shilin’s views in his later works, offering valuable insights into the changing attitudes of Qing mathematicians toward Western learning.

Keywords Luo Shilin; Bi Li Hui Tong; Jiu Zhang Suan Shu;